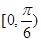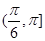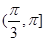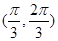题目内容
设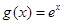 ,
,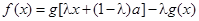 ,其中
,其中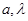 是常数,且
是常数,且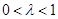 .
.
(1)求函数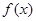 的极值;
的极值;
(2)证明:对任意正数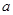 ,存在正数
,存在正数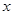 ,使不等式
,使不等式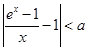 成立;
成立;
(3)设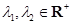 ,且
,且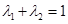 ,证明:对任意正数
,证明:对任意正数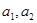 都有:
都有: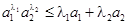 .
.
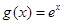 ,
,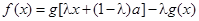 ,其中
,其中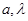 是常数,且
是常数,且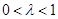 .
.(1)求函数
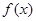 的极值;
的极值;(2)证明:对任意正数
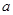 ,存在正数
,存在正数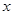 ,使不等式
,使不等式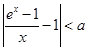 成立;
成立;(3)设
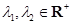 ,且
,且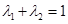 ,证明:对任意正数
,证明:对任意正数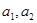 都有:
都有: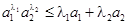 .
.(1)当 时,
时,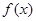 取极大值,但
取极大值,但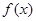 没有极小值(2)见解析(3)见解析
没有极小值(2)见解析(3)见解析
 时,
时,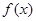 取极大值,但
取极大值,但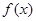 没有极小值(2)见解析(3)见解析
没有极小值(2)见解析(3)见解析(1)∵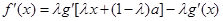 , -----------------1分
, -----------------1分
由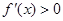 得,
得,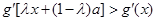 ,
,
∴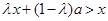 ,即
,即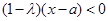 ,解得
,解得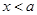 ,-----------------3分
,-----------------3分
故当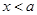 时,
时,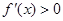 ;当
;当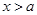 时,
时,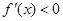 ;
;
∴当 时,
时,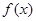 取极大值,但
取极大值,但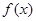 没有极小值.-----------------4分
没有极小值.-----------------4分
(2)∵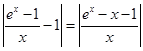 ,
,
又当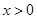 时,令
时,令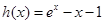 ,则
,则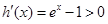 ,
,
故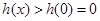 ,
,
因此原不等式化为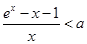 ,即
,即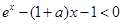 , -----------------6分
, -----------------6分
令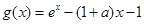 ,则
,则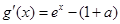 ,
,
由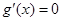 得:
得: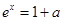 ,解得
,解得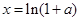 ,
,
当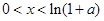 时,
时,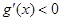 ;当
;当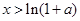 时,
时,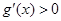 .
.
故当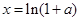 时,
时,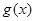 取最小值
取最小值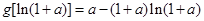 ,-----------------8分
,-----------------8分
令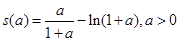 ,则
,则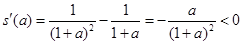 .
.
故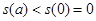 ,即
,即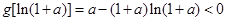 .
.
因此,存在正数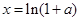 ,使原不等式成立.-----------------10分
,使原不等式成立.-----------------10分
(3)对任意正数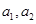 ,存在实数
,存在实数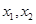 使
使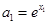 ,
,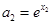 ,
,
则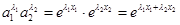 ,
,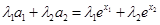 ,
,
原不等式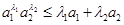
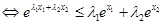 ,
,
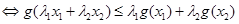 -----------------14分
-----------------14分
由(1)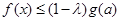 恒成立,
恒成立,
故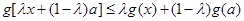 ,
,
取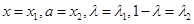 ,
,
即得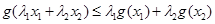 ,
,
即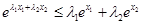 ,故所证不等式成立. -----------------14分
,故所证不等式成立. -----------------14分
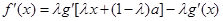 , -----------------1分
, -----------------1分由
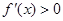 得,
得,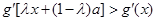 ,
,∴
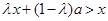 ,即
,即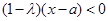 ,解得
,解得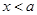 ,-----------------3分
,-----------------3分故当
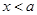 时,
时,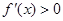 ;当
;当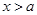 时,
时,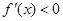 ;
;∴当
 时,
时,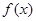 取极大值,但
取极大值,但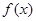 没有极小值.-----------------4分
没有极小值.-----------------4分(2)∵
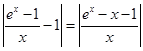 ,
,又当
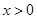 时,令
时,令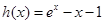 ,则
,则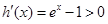 ,
,故
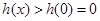 ,
,因此原不等式化为
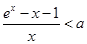 ,即
,即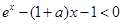 , -----------------6分
, -----------------6分令
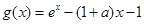 ,则
,则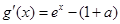 ,
,由
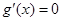 得:
得: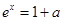 ,解得
,解得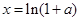 ,
,当
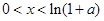 时,
时,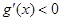 ;当
;当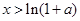 时,
时,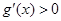 .
.故当
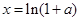 时,
时,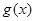 取最小值
取最小值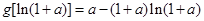 ,-----------------8分
,-----------------8分令
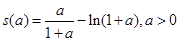 ,则
,则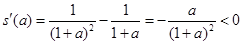 .
.故
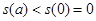 ,即
,即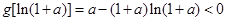 .
.因此,存在正数
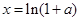 ,使原不等式成立.-----------------10分
,使原不等式成立.-----------------10分(3)对任意正数
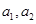 ,存在实数
,存在实数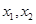 使
使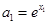 ,
,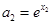 ,
,则
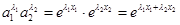 ,
,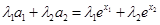 ,
,原不等式
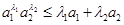
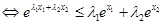 ,
,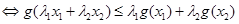 -----------------14分
-----------------14分由(1)
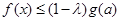 恒成立,
恒成立,故
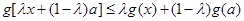 ,
,取
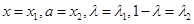 ,
,即得
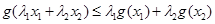 ,
,即
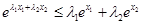 ,故所证不等式成立. -----------------14分
,故所证不等式成立. -----------------14分
练习册系列答案
相关题目
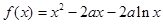 ,
,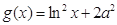 ,其中
,其中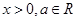 .
.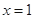 是函数
是函数 的极值点,求
的极值点,求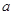 的值;
的值;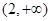 上单调递增,求
上单调递增,求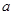 的取值范围;
的取值范围;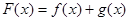 ,求证:
,求证: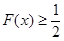 .
. 。
。 ,求
,求 在
在 处的切线方程;
处的切线方程; 的取值范围。
的取值范围。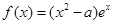 .
.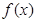 在
在 上不是单调函数,求实数
上不是单调函数,求实数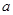 的取值范围;
的取值范围;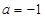 时,讨论函数
时,讨论函数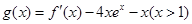 的零点个数.
的零点个数.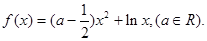
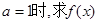 在区间
在区间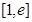 上的最大值和最小值;
上的最大值和最小值;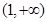 上,函数
上,函数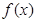 的图象恒在直线
的图象恒在直线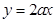 下方,求
下方,求 的取值范围.
的取值范围.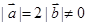 ,且关于
,且关于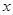 的函数
的函数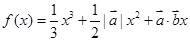 在
在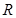 上有极值,则向量
上有极值,则向量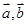 的夹角范围是( )
的夹角范围是( )