题目内容
已知数列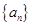 中,
中,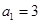 ,
,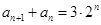 ,
,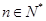 .
.
(1)证明:数列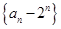 是等比数列,并求数列
是等比数列,并求数列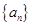 的通项公式;
的通项公式;
(2)在数列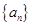 中,是否存在连续三项成等差数列?若存在,求出所有符合条件的项;若不存在,请说明理由;
中,是否存在连续三项成等差数列?若存在,求出所有符合条件的项;若不存在,请说明理由;
(3)若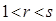 且
且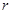 ,
,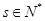 ,求证:使得
,求证:使得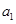 ,
,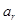 ,
,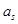 成等差数列的点列
成等差数列的点列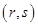 在某一直线上.
在某一直线上.
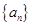 中,
中,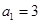 ,
,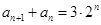 ,
,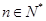 .
.(1)证明:数列
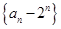 是等比数列,并求数列
是等比数列,并求数列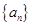 的通项公式;
的通项公式;(2)在数列
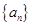 中,是否存在连续三项成等差数列?若存在,求出所有符合条件的项;若不存在,请说明理由;
中,是否存在连续三项成等差数列?若存在,求出所有符合条件的项;若不存在,请说明理由;(3)若
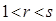 且
且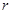 ,
,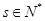 ,求证:使得
,求证:使得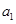 ,
,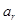 ,
,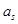 成等差数列的点列
成等差数列的点列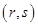 在某一直线上.
在某一直线上.(1)详见解析;(2)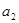 ,
,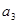 ,
,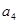 成等差数列;(3)详见解析.
成等差数列;(3)详见解析.
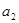 ,
,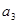 ,
,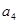 成等差数列;(3)详见解析.
成等差数列;(3)详见解析.试题分析:(1)证明一个数列为等比或等差数列,一般都是从定义入手,本小题首先需要将已知条件
 变形为
变形为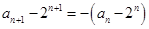 ,由于
,由于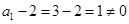 ,则
,则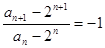 (常数),然后根据等比数列的定义可知数列
(常数),然后根据等比数列的定义可知数列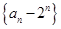 是以
是以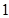 为首项,公比为
为首项,公比为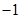 的等比数列,即
的等比数列,即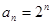
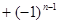 (
(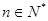 );
);(2)本小题首先假设在数列
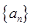 中存在连续三项
中存在连续三项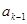 ,
,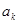 ,
,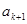 (
(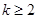 ,
,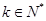 )成等差数列,则
)成等差数列,则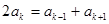 ,代入通项公式可得
,代入通项公式可得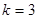 ,即
,即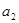 ,
,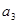 ,
,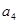 成等差数列.
成等差数列.(3)本小题首先根据
 ,
,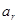 ,
,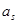 成等差数列,则
成等差数列,则 ,于是可得
,于是可得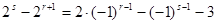 ,然后通过不定方程的分类讨论可得结论
,然后通过不定方程的分类讨论可得结论试题解析:(1)将已知条件
 变形为
变形为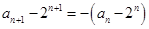 1分
1分由于
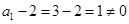 ,则
,则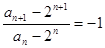 (常数) 3分
(常数) 3分即数列
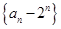 是以
是以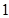 为首项,公比为
为首项,公比为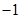 的等比数列 4分
的等比数列 4分所以

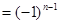 ,即
,即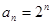
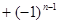 (
(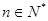 )。 5分
)。 5分(2)假设在数列
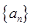 中存在连续三项成等差数列,
中存在连续三项成等差数列,不妨设连续的三项依次为
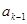 ,
,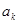 ,
,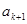 (
(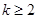 ,
,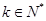 ),
),由题意得,
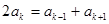 ,
,将
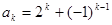 ,
, ,
,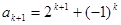 代入上式得 7分
代入上式得 7分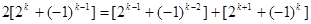 8分
8分化简得,
 ,即
,即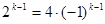 ,得
,得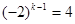 ,解得
,解得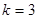
所以,存在满足条件的连续三项为
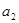 ,
,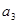 ,
,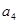 成等差数列。 10分
成等差数列。 10分(3)若
 ,
,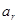 ,
,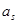 成等差数列,则
成等差数列,则
即
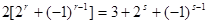 ,变形得
,变形得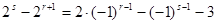 11分
11分由于若
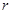 ,
,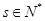 且
且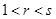 ,下面对
,下面对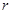 、
、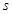 进行讨论:
进行讨论:① 若
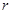 ,
,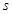 均为偶数,则
均为偶数,则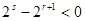 ,解得
,解得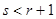 ,与
,与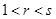 矛盾,舍去;
矛盾,舍去;② 若
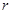 为奇数,
为奇数,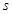 为偶数,则
为偶数,则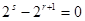 ,解得
,解得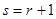 ;
;③ 若
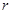 为偶数,
为偶数,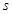 为奇数,则
为奇数,则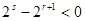 ,解得
,解得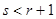 ,与
,与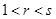 矛盾,舍去;
矛盾,舍去;④ 若
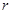 ,
,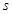 均为奇数,则
均为奇数,则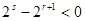 ,解得
,解得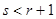 ,与
,与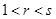 矛盾,舍去; 15分
矛盾,舍去; 15分综上①②③④可知,只有当
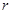 为奇数,
为奇数,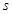 为偶数时,
为偶数时, ,
,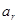 ,
,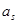 成等差数列,此时满足条
成等差数列,此时满足条件点列
 落在直线
落在直线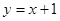 (其中
(其中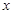 为正奇数)上。 16分(不写出直线方程扣1分)
为正奇数)上。 16分(不写出直线方程扣1分)
练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
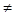 0的等差数列,且它的第2、3、6项依次构成等比数列{bn}的前3项。
0的等差数列,且它的第2、3、6项依次构成等比数列{bn}的前3项。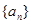 ,
,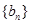 满足
满足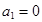 ,
,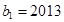 ,且对任意的正整数
,且对任意的正整数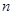 ,
,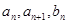 和
和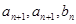 均成等比数列.
均成等比数列.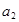 、
、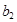 的值;
的值;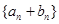 和
和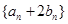 均成等比数列;
均成等比数列;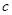 ,使得
,使得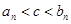 恒成立?证明你的结论.
恒成立?证明你的结论.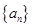 满足:
满足: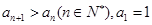 ,该数列的前三项分别加上l,l,3后顺次成为等比数列
,该数列的前三项分别加上l,l,3后顺次成为等比数列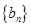 的前三项.
的前三项.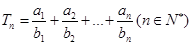 ,若
,若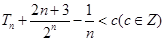 恒成立,求c的最小值.
恒成立,求c的最小值.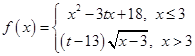 ,记
,记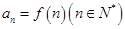 ,若
,若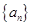 是递减数列,则实数
是递减数列,则实数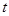 的取值范围是______________.
的取值范围是______________. 中,
中,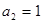 ,
, 则
则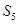 =( )
=( )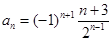 ,则该数列的第五项为( )
,则该数列的第五项为( )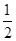
 满足
满足 ,
,
 ,则其通项
,则其通项 =( )
=( )



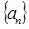 的前
的前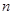 项和为
项和为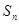 ,且
,且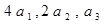 成等差数列。若
成等差数列。若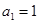 ,则
,则 。
。