题目内容
19.设f(x)=$\frac{{e}^{x}-{e}^{-x}}{2}$,g(x)=$\frac{{e}^{x}+{e}^{-x}}{2}$,求证:(1)g(2x)=[g(x)]2+[f(x)]2;
(2)求函数y=[f(x)]2+mg(x)最小值h(m).
分析 (1)运用指数的运算性质,由两边证,即可得到结论;
(2)求得函数的解析式,令t=$\frac{{e}^{x}+{e}^{-x}}{2}$(t≥1),则y=t2+mt-1,求出对称轴,讨论与区间[1,+∞)的关系,即可求得最小值.
解答 (1)证明:由g(2x)=$\frac{{e}^{2x}+{e}^{-2x}}{2}$,
[g(x)]2+[f(x)]2=($\frac{{e}^{x}+{e}^{-x}}{2}$)2+($\frac{{e}^{x}-{e}^{-x}}{2}$)2
=$\frac{{e}^{2x}+{e}^{-2x}+2}{4}$+$\frac{{e}^{2x}+{e}^{-2x}-2}{4}$=$\frac{{e}^{2x}+{e}^{-2x}}{2}$,
即有g(2x)=[g(x)]2+[f(x)]2;
(2)解:函数y=[f(x)]2+mg(x)=$\frac{{e}^{2x}+{e}^{-2x}-2}{4}$+m•$\frac{{e}^{x}+{e}^{-x}}{2}$,
可令t=$\frac{{e}^{x}+{e}^{-x}}{2}$(t≥1),则y=t2+mt-1,
对称轴为t=-$\frac{m}{2}$,
当-$\frac{m}{2}$≤1即m≥-2时,函数在[1,+∞)递增,
则最小值为h(m)=m;
当-$\frac{m}{2}$>1即m<-2时,函数在(1,-$\frac{m}{2}$)递减,在(-$\frac{m}{2}$,+∞)递增,
即有最小值h(m)=$\frac{-4-{m}^{2}}{4}$.
综上可得h(m)=$\left\{\begin{array}{l}{-1-\frac{{m}^{2}}{4},m<-2}\\{m,m≥-2}\end{array}\right.$.
点评 本题考查函数的最值的求法,注意运用换元法和分类讨论的思想方法,考查运算能力,属于中档题.

| A. | 2 | B. | 5 | C. | -1 | D. | -5 |
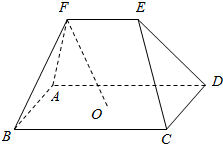 如图,在五面体ABCDE中,点O是平行四边形ABCD的对角线的交点,棱$EF\underline{\underline{∥}}\frac{1}{2}BC$
如图,在五面体ABCDE中,点O是平行四边形ABCD的对角线的交点,棱$EF\underline{\underline{∥}}\frac{1}{2}BC$