题目内容
8．
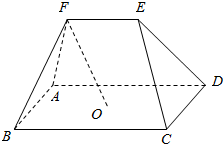如图，在五面体ABCDE中，点O是平行四边形ABCD的对角线的交点，棱$EF\underline{\underline{∥}}\frac{1}{2}BC$求证：FO∥平面CDE．
分析 要证明FO∥平面CDE，在平面CDE中：取CD中点M，连接OM．证明FO∥EM即可；
解答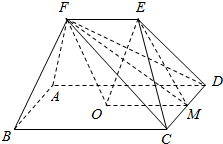 
证明：取CD中点M，连接OM，连接EM，
∵在矩形ABCD中，OM$\stackrel{∥}{=}$$\frac{1}{2}$BC，又EF$\stackrel{∥}{=}$$\frac{1}{2}$BC，
∴可得：EF$\stackrel{∥}{=}$OM，
∴四边形EFOM为平行四边形．
∴FO∥EM．
又因为FO?平面CDE，且EM?平面CDE，
∴FO∥平面CDE．
点评 本题考查直线与平面平行、直线与平面垂直等基础知识，考查空间想象能力和推理论证能力，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
3．如图程序是求10个数的平均数，则在横线上应填写的条件为（ ）
| A． | i＜1 | B． | i＞9 | C． | i＞10 | D． | i＜11 |
20．
某校高二学生有800名，从中抽取100名学生期末考试语文成绩的频率分布直方图如图所示，其中成绩分组区间是：[50，60），[60，70），[70，80），[80，90），[90，100]
（Ⅰ）求图中α的值；
（Ⅱ）根据频率分布直方图，估计这100名学生语文成绩的平均分、中位数、众数；（精确到个位数）
（Ⅲ）若这100名学生语文成绩某些分数段的人数（x）与数学成绩相应分数段的人数（y）之比如表所示，求推测高二这800名学生中数学成绩在[50，90）之外的人数．
某校高二学生有800名，从中抽取100名学生期末考试语文成绩的频率分布直方图如图所示，其中成绩分组区间是：[50，60），[60，70），[70，80），[80，90），[90，100]（Ⅰ）求图中α的值；
（Ⅱ）根据频率分布直方图，估计这100名学生语文成绩的平均分、中位数、众数；（精确到个位数）
（Ⅲ）若这100名学生语文成绩某些分数段的人数（x）与数学成绩相应分数段的人数（y）之比如表所示，求推测高二这800名学生中数学成绩在[50，90）之外的人数．
| 分数段 | [50，60） | [60，70） | [70，80） | [80，90） |
| x：y | 1：1 | 2：1 | 3：4 | 4：5 |