题目内容
5．已知二次函数f（x）的最小值为1，且f（0）=f（2）=3．（1）求f（x）的解析式；
（2）若f（x）在区间[2a，a+1]上是单调函数，求实数a的取值范围．
分析 （1）根据条件便知二次函数f（x）的对称轴为x=1，从而可设f（x）=a（x-1）2+1，根据f（0）=3便可得出a=2，这样便可得出f（x）的解析式；
（2）由f（x）的对称轴为x=1便可得出a满足$\left\{\begin{array}{l}{2a＜a+1}\\{2a≥1，或a+1≤1}\end{array}\right.$，解该不等式组便可得出实数a的取值范围．
解答 解：（1）由f（0）=f（2）知，f（x）的对称轴为x=1，f（x）的最小值为1；
∴设f（x）=a（x-1）2+1，由f（0）=3，得a=2；
∴f（x）=2（x-1）2+1；
（2）要使函数f（x）在[2a，a+1]上是单调函数，则：
$\left\{\begin{array}{l}{2a＜a+1}\\{2a≥1，或a+1≤1}\end{array}\right.$；
∴$\left\{\begin{array}{l}{a＜1}\\{a≥\frac{1}{2}，或a≤0}\end{array}\right.$；
即a≤0，或$\frac{1}{2}≤a＜1$；
∴实数a的取值范围为$（-∞，0]∪[\frac{1}{2}，1）$．
点评 考查二次函数的对称轴，二次函数的最小值，以及二次函数的单调性，清楚区间的定义．
练习册系列答案
相关题目
20．
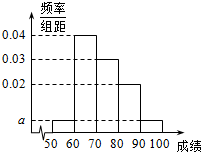某校高二学生有800名，从中抽取100名学生期末考试语文成绩的频率分布直方图如图所示，其中成绩分组区间是：[50，60），[60，70），[70，80），[80，90），[90，100]
（Ⅰ）求图中α的值；
（Ⅱ）根据频率分布直方图，估计这100名学生语文成绩的平均分、中位数、众数；（精确到个位数）
（Ⅲ）若这100名学生语文成绩某些分数段的人数（x）与数学成绩相应分数段的人数（y）之比如表所示，求推测高二这800名学生中数学成绩在[50，90）之外的人数．
某校高二学生有800名，从中抽取100名学生期末考试语文成绩的频率分布直方图如图所示，其中成绩分组区间是：[50，60），[60，70），[70，80），[80，90），[90，100]（Ⅰ）求图中α的值；
（Ⅱ）根据频率分布直方图，估计这100名学生语文成绩的平均分、中位数、众数；（精确到个位数）
（Ⅲ）若这100名学生语文成绩某些分数段的人数（x）与数学成绩相应分数段的人数（y）之比如表所示，求推测高二这800名学生中数学成绩在[50，90）之外的人数．
| 分数段 | [50，60） | [60，70） | [70，80） | [80，90） |
| x：y | 1：1 | 2：1 | 3：4 | 4：5 |