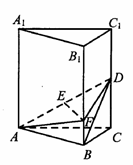
题目内容
在三棱锥 中,侧棱长均为
中,侧棱长均为 ,底边
,底边 ,
, ,
, ,
, 、
、 分别为
分别为 、
、 的中点.
的中点.

(1)求三棱锥 的体积;
的体积;
(2)求二面角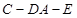 的平面角.
的平面角.
 中,侧棱长均为
中,侧棱长均为 ,底边
,底边 ,
, ,
, ,
, 、
、 分别为
分别为 、
、 的中点.
的中点.
(1)求三棱锥
 的体积;
的体积;(2)求二面角
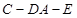 的平面角.
的平面角.(1)三棱锥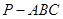 的体积为
的体积为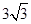 ;(2)二面角
;(2)二面角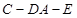 的平面角的大小为
的平面角的大小为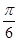 .
.
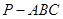 的体积为
的体积为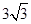 ;(2)二面角
;(2)二面角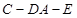 的平面角的大小为
的平面角的大小为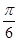 .
.试题分析:(1)由于三棱锥
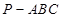 的侧棱长都相等,可以得到点
的侧棱长都相等,可以得到点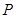 在平面
在平面 内的射影点为
内的射影点为 的外心,而由于
的外心,而由于 的三条底边满足勾股定理,可知
的三条底边满足勾股定理,可知 为直角三角形
为直角三角形 的斜边,从而可以知道
的斜边,从而可以知道 的中点
的中点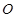 即为直角三角形
即为直角三角形 的外心,然后利用勾股定理求出
的外心,然后利用勾股定理求出 ,并且计算出直角三角形
,并且计算出直角三角形 的面积,最后利用锥体的体积公式计算此三棱锥的体积;(2)解法一是在(1)中的基础上,利用
的面积,最后利用锥体的体积公式计算此三棱锥的体积;(2)解法一是在(1)中的基础上,利用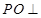 平面
平面 ,得到平面
,得到平面 平面
平面 ,然后在平面
,然后在平面 内作
内作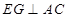 于点
于点 ,利用平面与平面垂直的性质定理得到
,利用平面与平面垂直的性质定理得到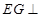 平面
平面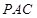 ,从而得到
,从而得到 ,再从点
,再从点 在平面
在平面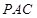 内作
内作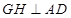 于点
于点 ,并连接
,并连接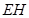 ,利用三垂线法得到
,利用三垂线法得到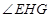 为二面角
为二面角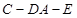 的平面角,最后在直角三角形
的平面角,最后在直角三角形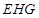 中计算
中计算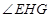 的大小;解法二是以
的大小;解法二是以 为原点,以
为原点,以 为
为 轴建立空间直角坐标系,利用空间向量法求二面角
轴建立空间直角坐标系,利用空间向量法求二面角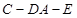 的平面角的大小.
的平面角的大小.试题解析:(1)取
 的中点
的中点 ,连接
,连接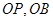 ,
, 易得:
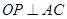 ,
,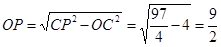 ,
,  ,
,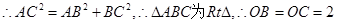 .
.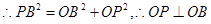 .
.又
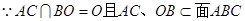

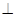 平面
平面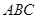 ,
,
(2)法一:作
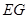 ⊥
⊥ ,
,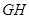 ⊥
⊥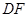 于
于 点,连接
点,连接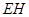
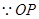
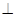 平面
平面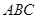 ,
,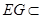 平面
平面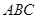 ,
,
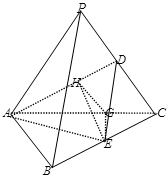
又
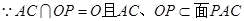

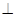 平面
平面 .
.∵
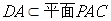 , ∴
, ∴
又
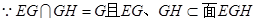

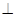 平面
平面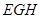 ,
,∵
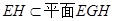 ,∴
,∴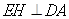 ,
,∴
 为二面角
为二面角 的平面角.
的平面角.∵
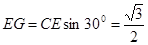 ,
,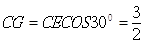 ,
,
由(Ⅰ)知
 ,
,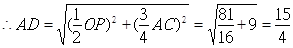 .
.∴
 ,
,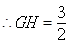
∴
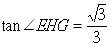 ,∴
,∴ ,
, 法二:以
 为原点,以
为原点,以 为
为 轴建系,则
轴建系,则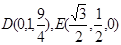 ,
,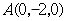 ,
, 设
 为平面
为平面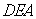 的法向量,则有
的法向量,则有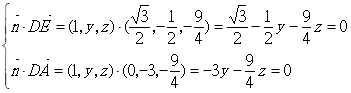 ,
,∴
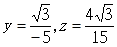
又∵
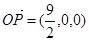 为平面
为平面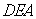 的法向量,
的法向量,∴
 ,二面角
,二面角 的平面角为
的平面角为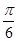 .
. 
练习册系列答案
相关题目
 的正方形ABCD中,E、F分别为BC、CD的中点,M、N分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合于B,构成一个三棱锥(如图所示).
的正方形ABCD中,E、F分别为BC、CD的中点,M、N分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合于B,构成一个三棱锥(如图所示).

 、
、 点,并判别MN与平面AEF的位置关系,并给出证明;
点,并判别MN与平面AEF的位置关系,并给出证明; 是线段
是线段 上一点,且
上一点,且 ,问是否存在点
,问是否存在点 ,若存在,求出
,若存在,求出 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
 ,
, ,PB与底面ABC成60°角,
,PB与底面ABC成60°角, 分别是
分别是 与
与 的中点,
的中点, 是线段
是线段 上任意一动点(可与端点重合),求多面体
上任意一动点(可与端点重合),求多面体 的体积。
的体积。 与直角梯形
与直角梯形 所在平面互相垂直,
所在平面互相垂直, ,
, ,
, .
.
 平面
平面 ;
; 的体积.
的体积. 中,
中, 分别为
分别为 、
、 的中点,
的中点, 为
为 上的点,且
上的点,且
 ∥平面
∥平面 ;
; ,
, ,求三棱锥
,求三棱锥 的体积.
的体积.



 ,过其球面上
,过其球面上 三点作截面,若
三点作截面,若 ,
, ,则球
,则球



 ,则该圆锥的侧面展开图的扇形圆心角等于_________.
,则该圆锥的侧面展开图的扇形圆心角等于_________. 的球体与棱柱的所有面均相切,那么这个三棱柱的表面积是( )
的球体与棱柱的所有面均相切,那么这个三棱柱的表面积是( )


