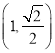题目内容
【题目】已知集合M={x|x2﹣4x+3＜0}，N={x||x﹣3|≤1}．
（1）求出集合M，N；
（2）试定义一种新集合运算△，使M△N={x|1＜x＜2}；
（3）若有P={x|| 
|≥ }，按（2）的运算，求出（N△M）△P．
【答案】
（1）解：M={x|x2﹣4x+3＜0}={x|1＜x＜3}，N={x||x﹣3|≤1}={x|2≤x≤4}
（2）解：M△N中的元素都在M中但不在N中，
∴定义M△N={x|x∈M且xN}
（3）解：P={x|| 
|≥ }=（2.5，3.5]，
∵N△M={x|3≤x≤4}，
∴（N△M）△P={x|3≤x≤4}
【解析】（1）利用不等式的解法，求出集合M，N；（2）M△N中的元素都在M中但不在N中；（3）P={x|| |≥ }=（2.5，3.5]，按（2）的运算，即可求出（N△M）△P．
练习册系列答案
相关题目
