题目内容
在三棱柱ABC-A1B1C1中，底面是正三角形，侧棱垂直于底面，若AB=
BB1，则AB1与C1B所成的角的大小为（ ）
| 2 |
分析：设BB1=1，则AB=
，将向量分解得
=
+
，
=
+
，结合题意算出数量积
•
=0，得到
⊥
，从而得出异面直线AB1与C1B所成的角的大小为90°．
| 2 |
| AB1 |
| AB |
| BB1 |
| C1B |
| C1C |
| CB |
| AB1 |
| C1B |
| AB1 |
| C1B |
解答：解：如图，设BB1=1，则AB=
，
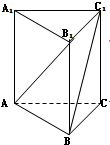
∵正三角形ABC中，∴∠ABC=60°
可得
•
=（
+
）•（
+
）
=
•
+
•
+
•
+
•
=0-1+|
|•|
|cos60°+0=-1+
•
cos60°=-1+1=0
因此，
⊥
，可得异面直线AB1与C1B所成的角的大小为90°
故选：B
| 2 |
∵正三角形ABC中，∴∠ABC=60°
可得
| AB1 |
| C1B |
| AB |
| BB1 |
| C1C |
| CB |
=
| AB |
| C1C |
| BB1 |
| C1C |
| AB |
| CB |
| BB1 |
| CB |
=0-1+|
| AB |
| CB |
| 2 |
| 2 |
因此，
| AB1 |
| C1B |
故选：B
点评：本题给出特殊的正三棱柱，求异面直线所成角的大小．着重考查了正三棱柱的性质、利用空间向量研究异面直线所成角的大小等知识，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
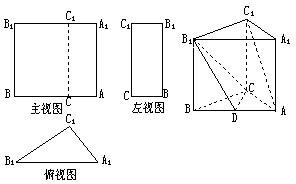已知三棱柱ABC-A1B1C1的三视图如图所示，其中主视图AA1B1B和左视图B1BCC1均为矩形，在俯视图△A1B1C1中，A1C1=3，A1B1=5，
如图：在正三棱柱ABC-A1 B1 C1中，AB=
在三棱柱ABC-A1B1C1中，已知AB=AC=AA1=
（2012•江西）在三棱柱ABC-A1B1C1中，已知AB=AC=AA1=
（2013•北京）如图，在三棱柱ABC-A1B1C1中，AA1C1C是边长为4的正方形．平面ABC⊥平面AA1C1C，AB=3，BC=5．