题目内容
 在三棱柱ABC-A1B1C1中,已知AB=AC=AA1=
在三棱柱ABC-A1B1C1中,已知AB=AC=AA1=| 5 |
(1)求点C到平面A1ABB1的距离;
(2)求二面角A-BC1-B1的余弦值;
(3)若M,N分别为直线AA1,B1C上动点,求MN的最小值.
分析:(1)利用点到平面的距离公式求距离.
(2)建立空间直角坐标系,利用向量法求二面角的大小.
(3)利用向量法求线段的长度.
(2)建立空间直角坐标系,利用向量法求二面角的大小.
(3)利用向量法求线段的长度.
解答: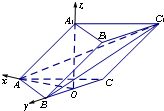 解:(1)连接AO,因为A1O⊥平面ABC,所以A1O⊥BC,因为AB=AC,OB=OC,
解:(1)连接AO,因为A1O⊥平面ABC,所以A1O⊥BC,因为AB=AC,OB=OC,
得AO⊥BC,AO=
=1,在△AOA1中,A1O=2,
在△BOA1中,A1B=2
,则S△A1AB=
.又S△CAB=2.
设点C到平面A1ABB1的距离为h,
则由VC-A1AB=VA1-ABC得,
S△A1AB•h=
S△CAB•A1O.从而h=
.…(4分)
(2)如图所示,分别以OA,OB,OA1所在的直线 为x,y,z轴,建立空间直角坐标系,
则A(1,0,0),C(0,-2,0),A1(0.0,2),B(0,2,0),B1(-1,2,2),C1(-1,-2,2).
设平面BCC1B1的法向量
=(x,y,z),
又
=(-1 ,0, 2),
=(0,4 , 0).
由
,得
,
令z=1,得x=2,y=0,即
=(2,0,1).
设平面ABC1的法向量
=(a,b,c),又
=(-1 ,2, 0),
=(-2,-2, 2).
由
,得
,令b=1,得a=2,c=3,即
=(2,1,3).
所以cos<
,
>=
=
,…(7分)
由图形观察可知,二面角A-BC1-B1为钝角,
所以二面角A-BC1-B1的余弦值是-
.…(9分)
(3)方法1.在△AOA1中,作OE⊥AA1于点E,因为AA1∥BB1,得OE⊥BB1.
因为A1O⊥平面ABC,所以A1O⊥BC,因为AB=AC,OB=OC,
得AO⊥BC,所以BC⊥平面AA1O,所以BC⊥OE,
所以OE⊥平面BB1C1C.从而OE⊥B1C
在△AOA1中,OE=
为异面直线AA1,B1C的距离,即为MN的最小值.…(14分)
方法2.设向量
1=(x1,y1,z1),且
1⊥
,
1⊥
∵
=(-1 ,0, 2),
=(1 ,-4, -2).
∴
1•
=-x1+2z1=0,
1•
x1-4y1-2z1=0.
令z1=1,得x1=2,y1=0,即
1=(2,0,1).
∵
=(-1,-2, 0).
所以异面直线AA1,B1C的距离d=|
|=
,即为MN的最小值.…(14分)
 解:(1)连接AO,因为A1O⊥平面ABC,所以A1O⊥BC,因为AB=AC,OB=OC,
解:(1)连接AO,因为A1O⊥平面ABC,所以A1O⊥BC,因为AB=AC,OB=OC,得AO⊥BC,AO=
| AB2-BO2 |
在△BOA1中,A1B=2
| 2 |
| 6 |
设点C到平面A1ABB1的距离为h,
则由VC-A1AB=VA1-ABC得,
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 6 |
(2)如图所示,分别以OA,OB,OA1所在的直线 为x,y,z轴,建立空间直角坐标系,
则A(1,0,0),C(0,-2,0),A1(0.0,2),B(0,2,0),B1(-1,2,2),C1(-1,-2,2).
设平面BCC1B1的法向量
| n |
又
| BB1 |
| CB |
由
|
|
令z=1,得x=2,y=0,即
| n |
设平面ABC1的法向量
| m |
| AB |
| AC1 |
由
|
|
| m |
所以cos<
| m |
| n |
| ||||
|
| ||
| 10 |
由图形观察可知,二面角A-BC1-B1为钝角,
所以二面角A-BC1-B1的余弦值是-
| ||
| 10 |
(3)方法1.在△AOA1中,作OE⊥AA1于点E,因为AA1∥BB1,得OE⊥BB1.
因为A1O⊥平面ABC,所以A1O⊥BC,因为AB=AC,OB=OC,
得AO⊥BC,所以BC⊥平面AA1O,所以BC⊥OE,
所以OE⊥平面BB1C1C.从而OE⊥B1C
在△AOA1中,OE=
2
| ||
| 5 |
方法2.设向量
| n |
| n |
| AA1 |
| n |
| B1C. |
∵
| AA1 |
| B1C |
∴
| n |
| AA1 |
| n |
| B1C= |
令z1=1,得x1=2,y1=0,即
| n |
∵
| AC |
所以异面直线AA1,B1C的距离d=|
| ||||
|
|
| 2 |
| 5 |
| 5 |
点评:本题主要考查利用向量法求二面角的大小和线段长度问题,要求熟练掌握相关的定理和公式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
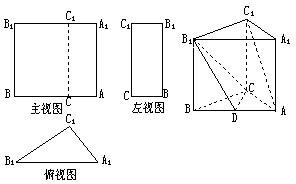 已知三棱柱ABC-A1B1C1的三视图如图所示,其中主视图AA1B1B和左视图B1BCC1均为矩形,在俯视图△A1B1C1中,A1C1=3,A1B1=5,
已知三棱柱ABC-A1B1C1的三视图如图所示,其中主视图AA1B1B和左视图B1BCC1均为矩形,在俯视图△A1B1C1中,A1C1=3,A1B1=5, 如图:在正三棱柱ABC-A1 B1 C1中,AB=
如图:在正三棱柱ABC-A1 B1 C1中,AB= (2012•江西)在三棱柱ABC-A1B1C1中,已知AB=AC=AA1=
(2012•江西)在三棱柱ABC-A1B1C1中,已知AB=AC=AA1= (2013•北京)如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.
(2013•北京)如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.