Question

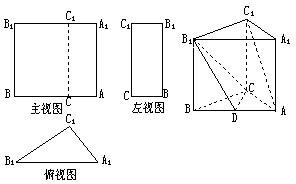已知三棱柱ABC-A₁B₁C₁的三视图如图所示，其中主视图AA₁B₁B和左视图B₁BCC₁均为矩形，在俯视图△A₁B₁C₁中，A₁C₁=3，A₁B₁=5，cos∠A1=

3

5

．
（1）在三棱柱ABC-A₁B₁C₁中，求证：BC⊥AC₁；
（2）在三棱柱ABC-A₁B₁C₁中，若D是底边AB的中点，求证：AC₁∥平面CDB₁．
（3）若三棱柱的高为5，求三视图中左视图的面积．

Answer 1

分析：（1）根据主视图和左视图均为矩形得到该三棱柱为直三棱柱，在俯视图△A₁B₁C₁中，利用余弦定理求出B₁C₁，从而得到BC⊥AC，而BC⊥CC₁，CC₁∩A₁C₁=C₁，根据线面垂直的判定定理可知BC⊥平面ACC₁A₁，而AC₁?平面ACC₁A₁，根据线面垂直的性质可知BC⊥AC₁．
（2）欲证AC₁∥平面CDB₁，根据直线与平面平行的判定定理可知只需证AC₁与平面CDB₁内一直线平行即可，连BC₁交B₁C于M，则M为BC₁的中点，连DM，根据中位线可知DM∥AC₁，而DM?平面DCB₁，AC₁?平面DCB₁，满足定理所需条件．
（3）左视图中BC的长等于底面△ABC中顶点C到边AB的距离d，求出a，最后根据矩形的面积公式求出所求即可．

解答：解：（1）因为主视图和左视图均为矩形、所以该三棱柱为直三棱柱，
在俯视图△A₁B₁C₁中，A₁C₁=3，A₁B₁=5，cos∠A1=

3

5

，
由余弦定理可得B₁C₁=4，
∴∠A₁C₁B₁=∠ACB=90°，
∴BC⊥AC
又∵BC⊥CC₁，CC₁∩A₁C₁=C₁，∴BC⊥平面ACC₁A₁．
∵AC₁?平面ACC₁A₁，∴BC⊥AC₁．
（2）连BC₁交B₁C于M，则M为BC₁的中点，连DM，则DM∥AC₁．
∵DM?平面DCB₁，AC₁?平面DCB₁，
∴AC₁∥平面CDB₁．
（3）左视图中BC的长等于底面△ABC中顶点C到边AB的距离d，d=

3×4

5

=

12

5

，
∴左视图的面积S=

12

5

×5=12．

点评：考查线面平行、线面垂直的判定定理以及面积的求法．涉及到的知识点比较多，知识性技巧性都很强．