题目内容
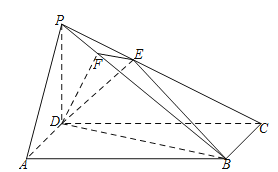
【题目】如图,四边形ABCD为菱形,G为AC与BD的交点,BE⊥平面ABCD,
(1)证明:平面AEC⊥平面BED.
(2)若∠ABC=120°,AE⊥EC,三棱锥E-ACD的体积为![]() ,求该三棱锥的侧面积.
,求该三棱锥的侧面积.
【答案】(1)见解析(2)3+2![]() .
.
【解析】试题分析:(1)由菱形性质得AC⊥BD.再由线面垂直性质得AC⊥BE,因此AC⊥平面BED.最后根据面面垂直判定定理得结论(2)先确定各面形状,再根据勾股定理求对应量,最后根据面积公式求各面面积,和为侧面积
试题解析:(1)因为四边形ABCD为菱形,所以AC⊥BD.
因为BE⊥平面ABCD,所以AC⊥BE,又BD∩BE=B,故AC⊥平面BED.
又AC平面AEC,所以平面AEC⊥平面BED.
(2)设AB=x,在菱形ABCD中,由∠ABC=120°,可得AG=GC=![]() x,GB=GD=
x,GB=GD=![]() .
.
因为AE⊥EC,所以在Rt△AEC中,可得EG=![]() x.
x.
由BE⊥平面ABCD,知△EBG为直角三角形,可得BE=![]() x.
x.
由已知得,三棱锥E-ACD的体积
VE-ACD=![]() ×
×![]() AC·GD·BE=
AC·GD·BE=![]() x3=
x3=![]() .
.
故x=2.从而可得AE=EC=ED=![]() .
.
所以△EAC的面积为3,△EAD的面积与△ECD的面积均为![]() .
.
故三棱锥E-ACD的侧面积为3+2![]() .
.

 特高级教师点拨系列答案
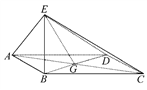
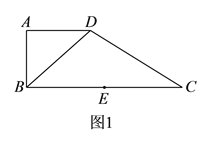
特高级教师点拨系列答案【题目】如图![]() ,在直角梯形
,在直角梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,点
,点![]() 是
是![]() 边的中点,将
边的中点,将![]() 沿
沿![]() 折起,使平面
折起,使平面![]() 平面
平面![]() ,连接
,连接![]() ,
, ![]() ,
, ![]() ,得到如图
,得到如图![]() 所示的几何体.
所示的几何体.
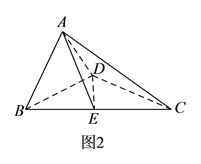
(Ⅰ)求证: ![]() 平面
平面![]() .
.
(Ⅱ)若![]() ,
, ![]() 与其在平面
与其在平面![]() 内的正投影所成角的正切值为
内的正投影所成角的正切值为![]() ,求点
,求点![]() 到平面
到平面![]() 的距离.
的距离.
【题目】某校随机调查80名学生,以研究学生爱好羽毛球运动与性别的关系,得到下面的![]() 列联表:
列联表:
爱好 | 不爱好 | 合计 | |
男 | 20 | 30 | 50 |
女 | 10 | 20 | 30 |
合计 | 30 | 50 | 80 |
(Ⅰ)将此样本的频率视为总体的概率,随机调查本校的3名学生,设这3人中爱好羽毛球运动的人数为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅱ)根据表3中数据,能否认为爱好羽毛球运动与性别有关?
| 0.050 | 0.010 |
| 3.841 | 6.635 |
附: ![]()