Question

已知半径为4的球面上有四点，S、A、B、C，且△ABC是等边三角形，球心O到平面ABC的距离为2，面SAB⊥面ABC，则棱锥S-ABC体积的最大值为（　　）

• A、9

  39

  +18

  3

• B、3

  39

  +6

  3

• C、3

  39

  +8

  3

• D、9

  39

  +6

  3

Answer 1

考点：棱柱、棱锥、棱台的体积

专题：计算题,空间位置关系与距离

分析：由于面SAB⊥面ABC，所以点S在平面ABC上的射影D落在AB上，D为AB中点时，SD最大，棱锥S-ABC的体积最大．运用线面垂直的性质，结合勾股定理，即可求得CD，AB，及SD，由三棱锥的体积公式即可得到最大值．

解答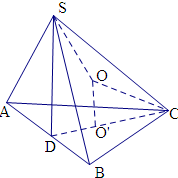： 解：由题意画出几何体的图形如图
由于面SAB⊥面ABC，所以点S在平面ABC上的射影D落在AB上，
由于OO′⊥平面ABC，SD⊥平面ABC，即有OO′∥SD，
当D为AB的中点时，SD最大，棱锥S-ABC的体积最大．
由于OC=4，OO′=2，则CO′=

16-4

=2

3

，
则DO'=

3

，则△ABC是边长为6的正三角形，
则△ABC的面积为：

3

4

×36=9

3

．
在直角梯形SDO′O中，SD=2+

42-( 3 )2

=2+

13

．
即有三棱锥S-ABC体积V=

1

3

×9

3

×（2+

13

）=6

3

+3

39

．
故选B．

点评：本题考查锥体体积计算，根据几何体的结构特征确定出S位置是关键．考查空间想象能力、计算能力．