题目内容
9.观察下列等式:$\frac{3}{1×2}×\frac{1}{2}=1-\frac{1}{2^2}$,
$\frac{3}{1×2}×\frac{1}{2}+\frac{4}{2×3}×\frac{1}{2^2}=1-\frac{1}{{3×{2^2}}}$,
$\frac{3}{1×2}×\frac{1}{2}+\frac{4}{2×3}×\frac{1}{2^2}+\frac{5}{3×4}×\frac{1}{2^3}=1-\frac{1}{{4×{2^3}}}$,
…,
由以上等式得$\frac{3}{1×2}×\frac{1}{2}+\frac{4}{2×3}×\frac{1}{2^2}+…+\frac{7}{5×6}×\frac{1}{2^5}$==$1-\frac{1}{{6×{2^5}}}$.
分析 根据题意,由每个等式的左边的变化规律,以及右边式子的变化规律,可得答案.
解答 解:由题意可知,得$\frac{3}{1×2}×\frac{1}{2}+\frac{4}{2×3}×\frac{1}{2^2}+…+\frac{7}{5×6}×\frac{1}{2^5}$=$1-\frac{1}{{6×{2^5}}}$,
故答案为:$1-\frac{1}{{6×{2^5}}}$
点评 本题考查了归纳推理,培养学生分析问题的能力.归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).

练习册系列答案
 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
4.下列函数求值算法中需要条件语句的函数是( )
| A. | f(x)=x3 | B. | f(x)=x2 | C. | f(x)=4x-x2 | D. | f(x)=$\left\{\begin{array}{l}{-1,x≥0}\\{1,x<0}\end{array}\right.$ |
1.设函数f(x)=ex+x-2的零点为x1,函数g(x)=lnx+x2-3的零点为x2,则( )
| A. | g(x1)<0,f(x2)>0 | B. | g(x1)>0,f(x2)<0 | C. | g(x1)>0,f(x2)>0 | D. | g(x1)<0,f(x2)<0 |
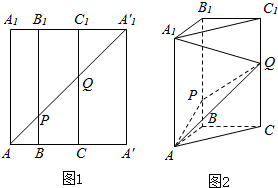 如图1所示,在边长为12的正方形AA′A′1A1中,BB1∥CC1∥AA1,且AB=3,BC=4,AA1′分别交BB1,CC1于点P,Q,将该正方形沿BB1、CC1折叠,使得A′A1′与AA1重合,构成如图2所示的三棱柱ABC-A1B1C1中
如图1所示,在边长为12的正方形AA′A′1A1中,BB1∥CC1∥AA1,且AB=3,BC=4,AA1′分别交BB1,CC1于点P,Q,将该正方形沿BB1、CC1折叠,使得A′A1′与AA1重合,构成如图2所示的三棱柱ABC-A1B1C1中