题目内容
如图,在正方体 中,
中, 分别为
分别为 ,
, ,
, ,
, 的中点,则异面直线
的中点,则异面直线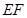 与
与 所成的角等于( )
所成的角等于( )
| A.45° | B.60° | C.90° | D.120° |
B
解析试题分析:将EF//A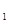 B,GH// C
B,GH// C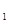 B,那么异面直线的的所成的角即为C
B,那么异面直线的的所成的角即为C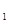 B,与A
B,与A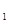 B的夹角。而结合正方体 性质可知,三角形A
B的夹角。而结合正方体 性质可知,三角形A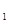 B C
B C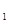 是等边三角形,故所成的夹角为60度,选B.
是等边三角形,故所成的夹角为60度,选B.
考点:本题主要考查了空间几何体中异面直线的所成角的求解的运用。
点评:解决该试题的关键是通过平移法来得到相交直线的夹角即为所求的异面直线的所成的角的求解的问题的运用。

练习册系列答案
相关题目
已知空间三条直线 若
若 与
与 异面,且
异面,且 与
与 异面,则( )
异面,则( )
A. 与 与 异面. 异面. | B. 与 与 相交. 相交. |
C. 与 与 平行. 平行. | D. 与 与 异面、相交、平行均有可能. 异面、相交、平行均有可能. |
若直线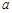 不平行于平面
不平行于平面 ,则下列结论成立的是( )
,则下列结论成立的是( )
A.平面 内的所有直线都与直线 内的所有直线都与直线 异面 异面 | B.平面 内不存在与直线 内不存在与直线 平行的直线 平行的直线 |
C.平面 内的直线都与直线 内的直线都与直线 相交 相交 | D.平面 内必存在直线与直线 内必存在直线与直线 垂直 垂直 |
已知 是两条不同直线,
是两条不同直线, 是三个不同平面,下列命题中正确的是( )
是三个不同平面,下列命题中正确的是( )
A. | B. |
C. | D. |
设l,m,n为三条不同的直线,α、β为两个不同的平面,下列命题中正确的个数是( )
① 若l⊥α,m∥β,α⊥β则l⊥m ② 若 则l⊥α
则l⊥α
③ 若l∥m,m∥n,l⊥α,则n⊥α ④ 若l∥m,m⊥α,n⊥β,α∥β,则l∥n
| A.1 | B.2 | C.3 | D.4 |
在三棱柱 中,各棱长相等,侧棱垂直于底面,点
中,各棱长相等,侧棱垂直于底面,点 是侧面
是侧面 的
的
中心,则 与平面
与平面 所成角的大小是( )
所成角的大小是( )
A. | B.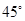 | C. | D.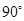 |
已知 、
、 是两条不同的直线,
是两条不同的直线,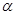 、
、 是两个不同的平面,则下面命题中正确的是( )
是两个不同的平面,则下面命题中正确的是( )
A. ∥ ∥ , , ∥ ∥  ∥ ∥ |
B.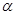 ∥ ∥  , ,  ∥ ∥ |
C.  |
D. ∥ ∥ , , 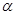   |
在正四棱柱 中,顶点
中,顶点 到对角线
到对角线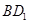 和到平面
和到平面 的距离分别为
的距离分别为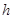 和
和 ,则下列命题中正确的是( )
,则下列命题中正确的是( )
A.若侧棱的长小于底面的边长,则 的取值范围为 的取值范围为 |
B.若侧棱的长小于底面的边长,则 的取值范围为 的取值范围为 |
C.若侧棱的长大于底面的边长,则 的取值范围为 的取值范围为 |
D.若侧棱的长大于底面的边长,则 的取值范围为 的取值范围为 |
已知在四面体 中,
中, 分别是
分别是 的中点,若
的中点,若 ,则
,则 与
与 所成的角的度数为( )
所成的角的度数为( )
A. | B. | C. | D. |