题目内容
在三棱柱 中,各棱长相等,侧棱垂直于底面,点
中,各棱长相等,侧棱垂直于底面,点 是侧面
是侧面 的
的
中心,则 与平面
与平面 所成角的大小是( )
所成角的大小是( )
A. | B.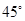 | C. | D.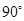 |
C
解析试题分析:取 的中点
的中点 ,由线面垂直的判定定理得
,由线面垂直的判定定理得 面
面 ,所以
,所以 与平面
与平面 所成的角是
所成的角是 设棱长为2
设棱长为2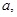 则
则 .所以
.所以 .
.
考点:棱柱的性质,直线与平面所成的角.
点评:找线面角关键是找出斜线在平面内的射影,并且角的范围为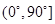 .
.

练习册系列答案
相关题目
在正方体ABCD-A1B1C1D1中与AD1成600角的面对角线的条数是( )
| A.4条 | B.6条 | C.8条 | D.10条 |
如图,在正方体 中,
中, 分别为
分别为 ,
, ,
, ,
, 的中点,则异面直线
的中点,则异面直线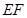 与
与 所成的角等于( )
所成的角等于( )
| A.45° | B.60° | C.90° | D.120° |
若m、n为两条不同的直线,α、β为两个不同的平面,则以下命题正确的是( ).
| A.若m∥α,n∥α,则m∥n | B.若m∥n,m⊥α,则n⊥α |
| C.若m∥β,α∥β,则m∥α | D.若α∩β=m,m⊥n,则n⊥α |
关于直线a,b,c以及平面M,N,给出下面命题:
①若a//M,b//M, 则a//b ②若a//M, b⊥M,则b⊥a ③若a M,b
M,b M,且c⊥a,c⊥b,则c⊥M ④若a⊥M, a//N,则M⊥N,其中正确命题的个数为( )
M,且c⊥a,c⊥b,则c⊥M ④若a⊥M, a//N,则M⊥N,其中正确命题的个数为( )
| A.0个 | B.1个 | C.2个 | D.3个 |
在正方体 中,E是棱
中,E是棱 的中点,则BE与平面
的中点,则BE与平面 所成角的正弦值为
所成角的正弦值为
A. | B. | C.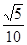 | D. |
若一个二面角的两个半平面与另一个二面角的两个半平面互相垂直,则这两个二面角的大小 ( )
| A.相等 | B.互补 | C.相等或互补 | D.无法确定 |




