题目内容
已知 、
、 是两条不同的直线,
是两条不同的直线,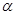 、
、 是两个不同的平面,则下面命题中正确的是( )
是两个不同的平面,则下面命题中正确的是( )
A. ∥ ∥ , , ∥ ∥  ∥ ∥ |
B.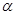 ∥ ∥  , ,  ∥ ∥ |
C.  |
D. ∥ ∥ , , 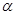   |
D
解析试题分析:因为若m?α,n?α,m∥β,n∥β,由于m,n不一定相交,故α∥β也不一定成立,故A错误;
若α∥β,m?α,m?β,则m,n可能平行也可能异面,故B错误;因为
 ,则根据一条直线垂直于平面内的两条直线,不一定线面垂直,必须m,n相交时成立,因此错误。
,则根据一条直线垂直于平面内的两条直线,不一定线面垂直,必须m,n相交时成立,因此错误。
若m∥n,n⊥α,根据线面垂直的第二判定定理,我们易得m⊥α,故D正确
考点:本试题主要考查了空间中点、线、面位置的关系的运用。
点评:解决该试题的关键是熟练的掌握空间中线面垂直的判定定理和面面平行的判定定理以及其性质定理的综合运用。准确翻译符号表示的图形,得到判定。

练习册系列答案
相关题目
在正方体 中,
中, 为
为 的交点,则
的交点,则 与
与 所成角的( )
所成角的( )
A. | B.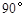 | C. | D. |
如图,在正方体 中,
中, 分别为
分别为 ,
, ,
, ,
, 的中点,则异面直线
的中点,则异面直线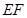 与
与 所成的角等于( )
所成的角等于( )
| A.45° | B.60° | C.90° | D.120° |
不同的直线a, b, c及不同的平面α,β,γ,下列命题正确的是( )
A.若a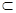 α,b α,b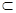 α,c⊥a, c⊥b 则c⊥α α,c⊥a, c⊥b 则c⊥α |
B.若b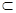 α, a//b则 a//α α, a//b则 a//α |
| C.若a⊥α, b⊥α 则a//b |
| D.若a//α,α∩β=b则a//b |
若m、n为两条不同的直线,α、β为两个不同的平面,则以下命题正确的是( ).
| A.若m∥α,n∥α,则m∥n | B.若m∥n,m⊥α,则n⊥α |
| C.若m∥β,α∥β,则m∥α | D.若α∩β=m,m⊥n,则n⊥α |
空间四边形ABCD中,若 ,则
,则 与
与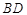 所成角为( )
所成角为( )
A. | B.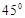 | C. | D. |
对于任意的直线 与平面
与平面 ,在平面
,在平面 内必有直线
内必有直线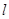 ,使
,使 与
与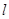 ( )
( )
| A.平行 | B.相交 | C.垂直 | D.互为异面直线 |
 中,下列几种说法正确的是 ( )
中,下列几种说法正确的是 ( )

 与
与 成
成 角
角 与
与 成
成 角
角
 、
、 为两个不同的平面,
为两个不同的平面, 、
、 、
、 为三条互不相同的直线,
为三条互不相同的直线, ,
, ,则
,则 ;
; ,
, ,
, ,
, ,则
,则 ;
; ,
, ,则
,则 ;
; ,
, ,
, ,则
,则 .
.