题目内容
【题目】我们要计算由抛物线
，x轴以及直线
所围成的区域的面积S，可用x轴上的分点
、
、
、…、
、1将区间
分成n个小区间，在每个小区间上做一个小矩形，使矩形的左端点在抛物线上，这些矩形的高分别为、
、
、…、
，矩形的底边长都是，设所有这些矩形面积的总和为
，为求S，只须令分割的份数n无限增大，就无限趋近于S，即
.
（1）求数列的通项公式，并求出S；
（2）利用相同的思想方法，探求由函数
的图象，x轴以及直线和
所围成的区域的面积T.
【答案】（1）
，
；（2）
.
【解析】
（1）计算出各小矩形面积，求和得
，再求极限得S；
（2）与（1）类似，只是小矩形的高换成
、
、
、…、
．
（1）由题意
，
；
（2）类似（1）将区间
等分成n个小区间，在每个小区间上做一个小矩形，小矩形的高依次为、、、…、．
，
．
小学夺冠AB卷系列答案
ABC考王全优卷系列答案
【题目】社区服务是高中学生社会实践活动的一个重要内容，汉中某中学随机抽取了100名男生、100名女生，了解他们一年参加社区服务的时间，按
，
，
，
，
（单位：小时）进行统计，得出男生参加社区服务时间的频率分布表和女生参加社区服务时间的频率分布直方图.
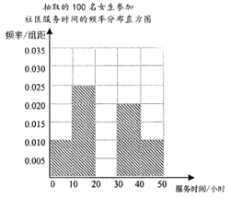
（1）完善男生参加社区服务时间的频率分布表和女生参加社区服务时间的频率分布直方图.
抽取的100名男生参加社区服务时间的频率分布表
社区服务时间 | 人数 | 频率 |
| 0.05 | |
| 20 | |
| 0.35 | |
| 30 | |
| ||
合计 | 100 | 1 |
学生社区服务时间合格与性别的列联表
不合格的人数 | 合格的人数 | |
男 | ||
女 |
（2）按高中综合素质评价的要求，高中学生每年参加社区服务的时间不少于20个小时才为合格，根据上面的统计图表，完成抽取的这200名学生参加社区服务时间合格与性别的列联表，并判断是否有
以上的把握认为参加社区服务时间达到合格程度与性别有关，并说明理由.
（3）用以上这200名学生参加社区服务的时间估计全市9万名高中学生参加社区服务时间的情况，并以频率作为概率.
（i）求全市高中学生参加社区服务时间不少于30个小时的人数.
（ⅱ）对我市高中生参加社区服务的情况进行评价.
参考公式
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.002 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
（
，其
）
