题目内容
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,点
轴正半轴为极轴,建立极坐标系,点![]() 为曲线
为曲线![]() 上的动点,点
上的动点,点![]() 在线段
在线段![]() 的延长线上,且满足
的延长线上,且满足![]() ,点
,点![]() 的轨迹为
的轨迹为![]() .
.
(1)求![]() ,
,![]() 的极坐标方程;
的极坐标方程;
(2)设点![]() 的极坐标为
的极坐标为![]() ,求△
,求△![]() 面积的最小值.
面积的最小值.
【答案】(1)曲线![]() 的极坐标方程为
的极坐标方程为![]() ,
,![]() 的极坐标方程为
的极坐标方程为![]() ;(2)
;(2)![]() .
.
【解析】
(1)消去参数,得到曲线![]() 的普通方程,进而根据极坐标方程与直角坐标方程的互化,即可得到曲线
的普通方程,进而根据极坐标方程与直角坐标方程的互化,即可得到曲线![]() 的极坐标方程,设点
的极坐标方程,设点![]() 的极坐标为
的极坐标为![]() ,点
,点![]() 的极坐标为
的极坐标为![]() ,根据极径的几何意义,利用
,根据极径的几何意义,利用![]() ,即可得到
,即可得到![]() 的极坐标方程.
的极坐标方程.
(2)由题设知![]() ,利用
,利用![]() ,即可求解.
,即可求解.
(1)∵曲线![]() 的参数方程为
的参数方程为![]() 为参数),
为参数),
∴曲线![]() 的普通方程为
的普通方程为![]() ,∴曲线
,∴曲线![]() 的极坐标方程为
的极坐标方程为![]() ,
,
设点![]() 的极坐标为
的极坐标为![]() ,点
,点![]() 的极坐标为
的极坐标为![]()
则![]() ,
,![]() ,
,![]() ,
,![]()
∵![]() ,
,![]() ,
,![]() ,即
,即![]() ,
,
∴![]() 的极坐标方程为
的极坐标方程为![]() .
.
(2)由题设知![]() ,
,
所以![]() ,
,
当![]() 时,
时,![]() 取得最小值为
取得最小值为![]() .
.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
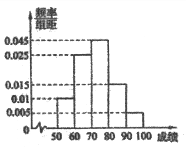
【题目】为了解人们对“延迟退休年龄政策”的态度,某部门从年龄在15岁到65岁的人群中随机调查了100人,并得到如图所示的频率分布直方图,在这100人中不支持“延迟退休年龄政策”的人数与年龄的统计结果如表所示:


(1)由频率分布直方图,估计这100人年龄的平均数;
(2)根据以上统计数据填写下面的2![]() 2列联表,据此表,能否在犯错误的概率不超过5%的前提下,认为以45岁为分界点的不同人群对“延迟退休年龄政策”的态度存在差异?
2列联表,据此表,能否在犯错误的概率不超过5%的前提下,认为以45岁为分界点的不同人群对“延迟退休年龄政策”的态度存在差异?
45岁以下 | 45岁以上 | 总计 | |
不支持 | |||
支持 | |||
总计 |
参考数据:
P(K2≥k0) | 0.100 | 0.050 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 6.635 | 10.828 |