题目内容
【题目】在四棱锥PABCD中,底面ABCD是正方形,侧棱PD垂直于底面ABCD,PD=DC,点E是PC的中点.
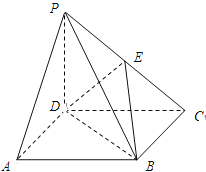
(Ⅰ)求证:PA∥平面EBD;
(Ⅱ)求二面角EBDP的余弦值.
【答案】(Ⅰ)详见解析;(Ⅱ)![]() .
.
【解析】
试题分析:(Ⅰ)几何法:连接![]() ,连接
,连接![]() ,根据线面平行的判定定理可先证明线线平行,即证明
,根据线面平行的判定定理可先证明线线平行,即证明![]() ;向量法:以点D为原点,DA为x轴,DC为y轴,DP为z轴建立直角坐标系,求平面
;向量法:以点D为原点,DA为x轴,DC为y轴,DP为z轴建立直角坐标系,求平面![]() 的法向量
的法向量![]() ,若
,若![]() ,说明
,说明![]() 与法向量垂直,即
与法向量垂直,即![]() 与平面平行;
与平面平行;
(Ⅱ)向量法求二面角的余弦值,即先求两个平面的法向量,而平面![]() 的法向量就是
的法向量就是![]() ,即求
,即求![]() .
.
试题解析:解:(Ⅰ)法一:以点D为原点,DA为x轴,DC为y轴,DP为z轴建立直角坐标系,设正方形的边长为1,则
![]()
∴![]() ,
,![]() .
.
设平面EBD的法向量为![]() ,
,
可求得![]() ,∴
,∴![]() ,∴
,∴![]() ∥平面EBD.
∥平面EBD.
即PA∥平面EBD.
法二:连接AC,设AC∩BD=O,连接OE,则OE∥PA,∴PA∥平面EBD.
(Ⅱ)设平面PBD的法向量为![]() .
.
∴![]() ,∴二面角E-BD-P的平面角的余弦值为
,∴二面角E-BD-P的平面角的余弦值为![]() .
.

【题目】某单位需要从甲、乙![]() 人中选拔一人参加新岗位培训,特别组织了
人中选拔一人参加新岗位培训,特别组织了![]() 个专项的考试,成绩统计如下:
个专项的考试,成绩统计如下:
第一项 | 第二项 | 第三项 | 第四项 | 第五项 | |
甲的成绩 |
|
|
|
|
|
乙的成绩 |
|
|
|
|
|
(1)根据有关统计知识,回答问题:若从甲、乙![]() 人中选出
人中选出![]() 人参加新岗培训,你认为选谁合适,请说明理由;
人参加新岗培训,你认为选谁合适,请说明理由;
(2)根据有关槪率知识,解答以下问题:
从甲、乙![]() 人的成绩中各随机抽取一个,设抽到甲的成绩为
人的成绩中各随机抽取一个,设抽到甲的成绩为![]() ,抽到乙的成绩为
,抽到乙的成绩为![]() ,用
,用![]() 表示满足条件
表示满足条件![]() 的事件,求事件
的事件,求事件![]() 的概率.
的概率.
【题目】某校对甲、乙两个文科班的数学考试成绩进行分析,规定:大于或等于120分为优秀,120分以下为非优秀.统计成绩后,得到如下的![]() 列联表,且已知在甲、乙两个文科班全部110人中随机抽1人为优秀的概率为
列联表,且已知在甲、乙两个文科班全部110人中随机抽1人为优秀的概率为![]() .
.
优秀 | 非优秀 | 合计 | |
甲班 | 10 | ||
乙班 | 30 | ||
合计 | 110 |
Ⅰ.请完成上面的列联表;
Ⅱ.根据列联表的数据,是否有![]() 的把握认为“成绩与班级有关系”.
的把握认为“成绩与班级有关系”.
参考公式与临界值表:![]() .
.


