题目内容
【题目】若正项数列![]() 满足:
满足:![]() ,则称此数列为“比差等数列”.
,则称此数列为“比差等数列”.
(1)试写出一个“比差等数列”的前![]() 项;
项;
(2)设数列![]() 是一个“比差等数列”,问
是一个“比差等数列”,问![]() 是否存在最小值,如存在,求出最小值;如不存在,请说明理由;
是否存在最小值,如存在,求出最小值;如不存在,请说明理由;
(3)已知数列![]() 是一个“比差等数列”,
是一个“比差等数列”,![]() 为其前
为其前![]() 项的和,试证明:
项的和,试证明:![]() .
.
【答案】(1)![]() 、
、![]() 、
、![]() (答案不唯一);(2)存在,且
(答案不唯一);(2)存在,且![]() 的最小值为
的最小值为![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】
(1)根据“比差等数列”的定义得出![]() ,由
,由![]() ,可得出
,可得出![]() ,然后对
,然后对![]() 取一个大于
取一个大于![]() 的值,可得出一个符合条件的“比差等数列”
的值,可得出一个符合条件的“比差等数列”![]() 的前
的前![]() 项;
项;
(2)由题意得出![]() ,且
,且![]() ,利用基本不等式可求出
,利用基本不等式可求出![]() 的最小值;
的最小值;
(3)由![]() 可推出
可推出![]() ,利用数学归纳法证明
,利用数学归纳法证明![]() ,由此得出
,由此得出![]() ,
,![]() 、
、![]() 、
、![]() 、
、![]() ,然后利用同向不等式的可加性可证明出
,然后利用同向不等式的可加性可证明出![]() 成立.
成立.
(1)由于数列![]() 为“比差等数列”,则
为“比差等数列”,则![]() ,可得
,可得![]() .
.
由于数列![]() 每项都是正数,则
每项都是正数,则![]() ,可得出
,可得出![]() .
.
若![]() ,则
,则![]() ,
,![]() .
.
因此,“比差等数列”的前![]() 项可以是
项可以是![]() 、
、![]() 、
、![]() (答案不唯一);
(答案不唯一);
(2)由(1)可知,![]() ,则
,则![]() ,
,
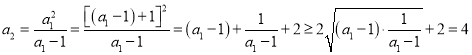 ,
,
当且仅当![]() 时,等号成立,因此,
时,等号成立,因此,![]() 有最小值
有最小值![]() ;
;
(3)由题意可得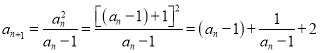 .
.
由于双勾函数![]() 在
在![]() 上是增函数,
上是增函数,
![]() ,
,![]() ,且
,且![]() ,则
,则![]() ,
,
同理可得![]() .
.
猜想,当![]() 时,
时,![]() .
.
假设当![]() 时,猜想成立,即
时,猜想成立,即![]() ;
;
那么当![]() 时,由于函数
时,由于函数![]() 在
在![]() 上是增函数,
上是增函数,
且![]() ,
,
所以,![]() .
.
由归纳原理可知,当![]() 时,
时,![]() .
.
于是有![]() ,
,![]() 、
、![]() 、
、![]() 、
、![]() ,
,
将上述不等式全部相加得![]() .
.
因此,![]() .
.

【题目】为了解某校学生参加社区服务的情况,采用按性别分层抽样的方法进行调查.已知该校共有学生960人,其中男生560人,从全校学生中抽取了容量为n的样本,得到一周参加社区服务的时间的统计数据如下表:
超过1小时 | 不超过1小时 | |
男 | 20 | 8 |
女 | 12 | m |
(1)求m,n;
(2)能否有95多的把握认为该校学生一周参加社区服务时间是否超过1小时与性别有关?
(3)以样本中学生参加社区服务时间超过1小时的频率作为该事件发生的概率,现从该校学生中随机调查6名学生,试估计6名学生中一周参加社区服务时间超过1小时的人数.
附:
| 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |

【题目】为考查某种疫苗预防疾病的效果,进行动物实验,得到统计数据如下:
未发病 | 发病 | 总计 | |
未注射疫苗 | 20 |
|
|
注射疫苗 | 30 |
|
|
总计 | 50 | 50 | 100 |
现从所有试验动物中任取一只,取到“注射疫苗”动物的概率为![]() .
.
(1)求![]() 列联表中的数据
列联表中的数据![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
(2)判断疫苗是否有效?
(3)能够有多大把握认为疫苗有效?
(参考公式![]() ,
,![]() )
)
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |


