题目内容
10.函数y=22x-4•2x的值域是[-4,+∞).分析 利用换元法结合指数函数,一元二次函数的性质进行求解即可.
解答 解:∵y=22x-4•2x=y=(2x)2-4•2x,
∴令t=2x,则t>0,
则函数等价为y=t2-4t=(t-2)2-4,
∵t>0,
∴y≥-4,
即函数的值域为[-4,+∞).
故答案为:[-4,+∞)
点评 本题主要考查函数值域的求解,利用换元法结合一元二次函数和指数函数的性质是解决本题的关键.

练习册系列答案
 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
18.已知函数f(x)=$\left\{\begin{array}{l}{lo{g}_{2}x\\;x>0}\\{{2}^{x}\\;x≤0}\end{array}\right.$,若f(1)+f(a)=2,则a的值为( )
| A. | 1 | B. | 2 | C. | 4 | D. | 4或1 |
15.复数1+$\sqrt{3}$i的三角形式是( )
| A. | cos$\frac{π}{3}$+isin$\frac{π}{3}$ | B. | 2(cos$\frac{π}{3}$+isin$\frac{π}{3}$) | C. | cos$\frac{π}{6}$+isin$\frac{π}{6}$ | D. | 2(cos$\frac{π}{6}$+isin$\frac{π}{6}$) |
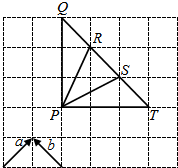 如图所示,下列结论正确的是( )
如图所示,下列结论正确的是( )