题目内容
(12分)
如图,平面ABEF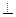 平面ABCD,四边形ABEF与ABCD都是直角梯形,
平面ABCD,四边形ABEF与ABCD都是直角梯形,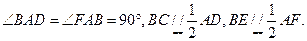
(I)证明:C,D,F,E四点共面;
(II)设AB=BC=BE,求二面角A—ED—B的大小。
如图,平面ABEF
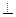 平面ABCD,四边形ABEF与ABCD都是直角梯形,
平面ABCD,四边形ABEF与ABCD都是直角梯形,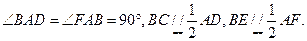
(I)证明:C,D,F,E四点共面;
(II)设AB=BC=BE,求二面角A—ED—B的大小。

(1)略
(2)
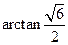
解:法1:(Ⅰ)解:延长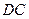 交
交 的延长线于点
的延长线于点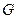 ,
,
由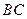
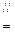
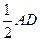 得
得
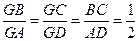 ……2分
……2分
延长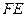 交
交 的延长线于
的延长线于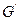 同理可得
同理可得
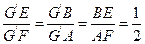
故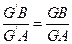 ,即
,即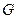 与
与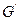 重合……4分
重合……4分
因此直线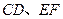 相交于点
相交于点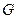 ,即
,即 四点共面。……6分
四点共面。……6分
(Ⅱ)证明:设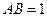 ,则
,则 ,
,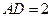
取 中点
中点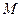 ,则
,则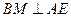 ,
,
又由已知得,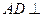 平面
平面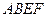
故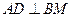 ,
,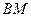 与平面
与平面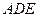 内两相交直线
内两相交直线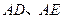 都垂直。
都垂直。
所以 平面
平面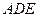 ,作
,作 ,垂足为
,垂足为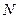 ,连结
,连结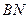
由三垂线定理知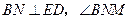 为二面角
为二面角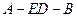 的平面角。……9分
的平面角。……9分
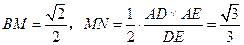
 故
故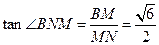
所以二面角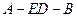 的大小
的大小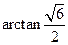 ……12分
……12分
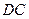 交
交 的延长线于点
的延长线于点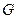 ,
,由
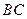
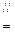
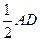 得
得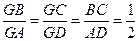 ……2分
……2分延长
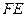 交
交 的延长线于
的延长线于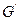 同理可得
同理可得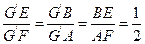
故
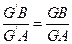 ,即
,即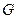 与
与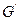 重合……4分
重合……4分因此直线
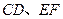 相交于点
相交于点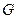 ,即
,即 四点共面。……6分
四点共面。……6分(Ⅱ)证明:设
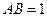 ,则
,则 ,
,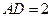
取
 中点
中点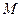 ,则
,则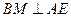 ,
,又由已知得,
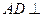 平面
平面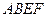
故
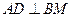 ,
,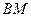 与平面
与平面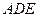 内两相交直线
内两相交直线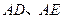 都垂直。
都垂直。所以
 平面
平面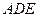 ,作
,作 ,垂足为
,垂足为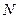 ,连结
,连结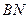
由三垂线定理知
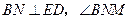 为二面角
为二面角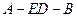 的平面角。……9分
的平面角。……9分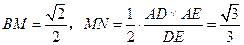
 故
故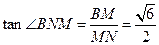
所以二面角
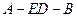 的大小
的大小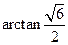 ……12分
……12分
练习册系列答案
相关题目
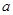 ,高为
,高为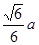 ,则此棱锥的侧面积等于( )
,则此棱锥的侧面积等于( )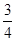
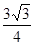

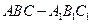 中,侧面
中,侧面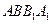 ,
,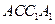 均为正方形,∠
均为正方形,∠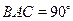 ,点
,点 是棱
是棱 的中点.
的中点.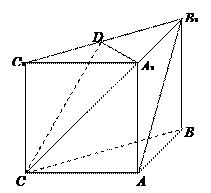
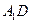 ⊥平面
⊥平面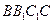 ;
;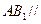 平面
平面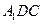 ;
;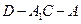 的余弦值
的余弦值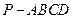 中,顶点
中,顶点 在底面
在底面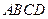 上的射影恰好落在
上的射影恰好落在 的中点
的中点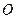 上,又∠
上,又∠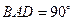 ,
,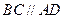 ,且
,且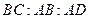
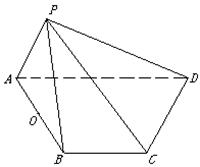
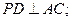
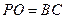 , 求直线
, 求直线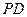 与
与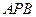 与平面
与平面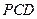 所成的角为
所成的角为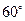 , 求
, 求 的值
的值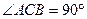 ,E、F分别是BA、BC的中点,G是AA1上一点,且
,E、F分别是BA、BC的中点,G是AA1上一点,且

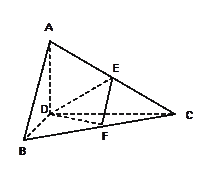
 的边长为4,
的边长为4, 是
是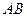 边上的高,
边上的高, 分别是
分别是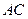 和
和 边的中点,现将△
边的中点,现将△ .
. 的位置关系,并说明理由;
的位置关系,并说明理由; 的余弦值;
的余弦值; ,使
,使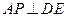 ?证明你的结论.
?证明你的结论.
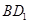 是正方体
是正方体 的一条对角线,则这个正方体中面对角线与
的一条对角线,则这个正方体中面对角线与
