题目内容
【题目】为了弘扬民族文化，某校举行了“我爱国学，传诵经典”考试，并从中随机抽取了100名考生的成绩（得分均为整数,满足100分）进行统计制表，其中成绩不低于80分的考生被评为优秀生，请根据频率分布表中所提供的数据，用频率估计概率，回答下列问题.
分组 | 频数 | 频率 |
| 5 | 0.05 |
|
| 0.20 |
| 35 |
|
| 25 | 0.25 |
| 15 | 0.15 |
合计 | 100 | 1.00 |
（1）求
的值及随机抽取一考生恰为优秀生的概率；
（2）按频率分布表中的成绩分组，采用分层抽样抽取20人参加学校的“我爱国学”宣传活动，求其中优秀生的人数；
（3）在第（2）问抽取的优秀生中指派2名学生担任负责人，求至少一人的成绩在
的概率.
【答案】（Ⅰ）0.4．（Ⅱ）8人．（Ⅲ） 
．
【解析】试题分析：（Ⅰ）由频率分布表，列出方程
，求得
的值，即可求解概率；
（Ⅱ）根据分层抽样，直接求解即可．
（Ⅲ）根据题意求得基本事件的总数，利用古典概型概率的求解公式，即可求解概率值．
试题解析：
（Ⅰ）由频率分布表得： 
，解得a=20，b=0.35，
由频率分布表可得随机抽取一考生恰为优秀生的概率为：P=0.25+0.15=0.4．
（Ⅱ）按成绩分层抽样抽取20人时，优秀生应抽取20×0.4=8人．
（Ⅲ）8人中，成绩在[80，90）的有：20×0.25=5人，成绩在[90，100]的有：20×0.15=3
人，从8个人中选2个人，结果共有n=
=28种选法，
其中至少有一人成绩在[90，100]的情况有两种：
可能有1人成绩在[90，100]，也可能有2人成绩在[90，100]，所以共有5×3+3=18种，
∴至少一人的成绩在[90，100]的概率
．
【题目】在一次抽样调查中测得样本的6组数据，得到一个变量
关于
的回归方程模型，其对应的数值如下表：
| 2 | 3 | 4 | 5 | 6 | 7 |
|
|
|
|
|
|
|
(1)请用相关系数
加以说明与之间存在线性相关关系(当
时，说明与之间具有线性相关关系)；
(2)根据(1)的判断结果，建立关于的回归方程并预测当
时，对应的值为多少(
精确到
).
附参考公式：回归方程
中斜率和截距的最小二乘法估计公式分别为：
，
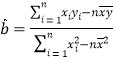，相关系数公式为：
.
参考数据：
，
，
，
.
【题目】某校计划面向高一年级1240名学生开设校本选修课程，为确保工作的顺利实施，按性别进行分层抽样，现抽取124名学生对社会科学类、自然科学类这两大类校本选修课程进行选课意向调查，其中男生有65人.在这124名学生中选修社会科学类的男生有22人、女生有40人.
（1）根据以上数据完成下列列联表；
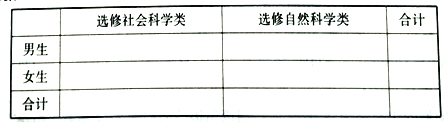
（2）判断能否有99.9%的把握认为科类的选修与性别有关？
附：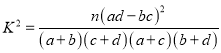 
，其中
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
