题目内容
【题目】已知四棱柱ABCD﹣A1B1C1D1的底面是边长为2的菱形,且∠BAD= ![]() ,AA1⊥平面ABCD,AA1=1,设E为CD中点
,AA1⊥平面ABCD,AA1=1,设E为CD中点 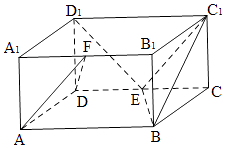
(1)求证:D1E⊥平面BEC1
(2)点F在线段A1B1上,且AF∥平面BEC1 , 求平面ADF和平面BEC1所成锐角的余弦值.
【答案】
(1)证明:由已知该四棱柱为直四棱柱,且△BCD为等边三角,BE⊥CD
所以BE⊥平面CDD1C1,而D1E平面CDD1C1,故BE⊥D1E
因为△C1D1E的三边长分别为 ![]() ,故△C1D1E为等腰直角三角形
,故△C1D1E为等腰直角三角形
所以D1E⊥C1E,结合D1E⊥BE知:D1E⊥平面BEC1
(2)解:取AB中点G,则由△ABD为等边三角形
知DG⊥AB,从而DG⊥DC
以DC,DG,DD1为坐标轴,建立如图所示的坐标系
此时 ![]() ,
, ![]() ,设
,设 ![]()
由上面的讨论知平面BEC1的法向量为 ![]()
由于AF平面BEC1,故AF∥平面BEC1 ![]()
故(λ+1,0,1)(1,0,﹣1)=(λ+1)﹣1=0λ=0,故 ![]()
设平面ADF的法向量为 ![]() ,
, ![]()
由 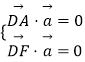 知
知 ![]() ,取
,取 ![]() ,故
,故 ![]()
设平面ADF和平面BEC1所成锐角为θ,则 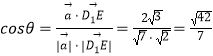
即平面ADF和平面BEC1所成锐角的余弦值为 ![]() .
.

【解析】(1)推导出BE⊥D1E,D1E⊥C1E,由此能证明D1E⊥平面BEC1 . (2)取AB中点G,则由△ABD为等边三角形知DG⊥AB,从而DG⊥DC,以DC,DG,DD1为坐标轴,建立空间直角坐标系,利用向量法能求出平面ADF和平面BEC1所成锐角的余弦值.
【考点精析】解答此题的关键在于理解直线与平面垂直的判定的相关知识,掌握一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.

 阅读快车系列答案
阅读快车系列答案