题目内容
14．
如图，AB是半径为2的圆O的弦，CD是圆O的切线，C是切点，D是OB的延长线与CD的交点，CD∥AB，若CD=$\sqrt{5}$，则AC等于（ ）| A． | $\frac{\sqrt{6}}{3}$ | B． | $\frac{2\sqrt{6}}{3}$ | C． | 1 | D． | 2 |
分析 连接OC，则OC⊥CD，利用CD∥AB，可得OC⊥AB，AC=BC，利用余弦定理求出BC，即可得出结论．
解答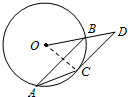 
解：连接OC，则OC⊥CD，
∵CD∥AB，∴OC⊥AB，
∴AC=BC，
△OCD中，OC=2，CD=$\sqrt{5}$，∴OD=3，
∴BD=1，cos∠D=$\frac{\sqrt{5}}{3}$，
∴BC=$\sqrt{1+5-2×1×\sqrt{5}×\frac{\sqrt{5}}{3}}$=$\frac{2\sqrt{6}}{3}$，
∴AC=$\frac{2\sqrt{6}}{3}$，
故选：B．
点评 本题考查圆的切线的性质，考查余弦定理，考查学生的计算能力，属于中档题．
练习册系列答案
相关题目
4．已知sin（x+$\frac{π}{6}$）=$\frac{1}{4}$，则sin（$\frac{5π}{6}$-x）+sin2（$\frac{π}{3}$-x）的值为（ ）
| A． | -$\frac{3}{16}$ | B． | $\frac{5}{16}$ | C． | $\frac{15}{16}$ | D． | $\frac{19}{16}$ |
2．在△ABC中，内角A、B、C的对边分别是a，b，c，若sin2A+sin2B-sin2C=0，a2+c2-b2-ac=0，c=2，则a=（ ）
| A． | 1 | B． | $\sqrt{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{\sqrt{3}}{2}$ |
如图，△ABC是圆内接三角形，∠BAC的平分线交圆于点D，交BC于点F，过点B圆的切线与CD的延长线交于点E．
1．sin80°cos20°-cos80°sin20°的值为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | -$\frac{1}{2}$ | D． | -$\frac{\sqrt{3}}{2}$ |
2．已知动点P与平面上两定点A（-$\sqrt{2}$，0），B（$\sqrt{2}$，0）连线的斜率的积为定值-$\frac{1}{2}$．则动点P的轨迹方程C（ ）
| A． | $\frac{{x}^{2}}{5}$$+\frac{{y}^{2}}{9}$=1 | B． | $\frac{{x}^{2}}{2}$+y2=1 | C． | $\frac{{x}^{2}}{16}$$+\frac{{y}^{2}}{16}$=1 | D． | $\frac{{x}^{2}}{16}$$+\frac{{y}^{2}}{9}$=1 |