题目内容
19.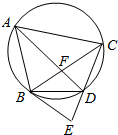 如图,△ABC是圆内接三角形,∠BAC的平分线交圆于点D,交BC于点F,过点B圆的切线与CD的延长线交于点E.
如图,△ABC是圆内接三角形,∠BAC的平分线交圆于点D,交BC于点F,过点B圆的切线与CD的延长线交于点E.(1)求证;∠EBD=∠CBD.
(2)若DE=2,DC=3,求边BC的长.
分析 (1)利用角与弧的关系,得到角相等;
(2)利用角相等推导出三角形相似,得到边成比例,即可得出结论.
解答 (1)证明:∵BE是切线,由弦切角定理,∴∠EBD=∠DAB …(1分)
∵∠DAC,∠CBD是同弧上的圆周角,∴∠CBD=∠DAC …(2分)
∵AD是∠BAC的平分线,∴∠DAB=∠DAC …(3分)
∴∠EBD=∠CBD …(4分)
(2)解:∵BE是切线,由切割线定理,EB2=ED•EC=10,
∴EB=$\sqrt{10}$…(6分)
由弦切角定理,∠EBD=∠DCB …(7分)
∴由(1)知,∠EBD=∠CBD=∠DCB,∴DC=DB=3 …(8分)
∵∠BED=∠CED,
∴△BED∽△CEB …(10分)
∴$\frac{BC}{BD}=\frac{EC}{BE}$,∴$\frac{BC}{3}=\frac{5}{\sqrt{10}}$,
∴BC=$\frac{3\sqrt{10}}{2}$ …(12分)
点评 本题考查了弦切角、圆周角与弧的关系,还考查了三角形相似的知识,本题总体难度不大,属于中档题.

练习册系列答案
相关题目
10.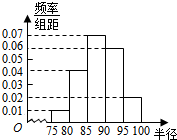 某盒里有20个球,其半径大小的频率分布直方图如图所示.
某盒里有20个球,其半径大小的频率分布直方图如图所示.
(Ⅰ)下表是这些球的半径的频数分布表,求正整数a,b的值;
(Ⅱ)半径在[90,95)和[95,100)里的球分别用1,2,3,…标记,现从这两个区间里的球中各摸出一球.
①若用x表示从区间[90,95)中摸出的球的号码,y表示从区间[95,100)中摸出的球的号码,请写出数对(x,y)的所有情形;
②求这两球的号码之和大于5的概率.
 某盒里有20个球,其半径大小的频率分布直方图如图所示.
某盒里有20个球,其半径大小的频率分布直方图如图所示.(Ⅰ)下表是这些球的半径的频数分布表,求正整数a,b的值;
| 区间 | [75,80) | [80,85) | [85,90) | [90,95) | [95,100] |
| 人数 | 1 | a | 7 | 6 | b |
①若用x表示从区间[90,95)中摸出的球的号码,y表示从区间[95,100)中摸出的球的号码,请写出数对(x,y)的所有情形;
②求这两球的号码之和大于5的概率.
14.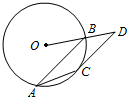 如图,AB是半径为2的圆O的弦,CD是圆O的切线,C是切点,D是OB的延长线与CD的交点,CD∥AB,若CD=$\sqrt{5}$,则AC等于( )
如图,AB是半径为2的圆O的弦,CD是圆O的切线,C是切点,D是OB的延长线与CD的交点,CD∥AB,若CD=$\sqrt{5}$,则AC等于( )
 如图,AB是半径为2的圆O的弦,CD是圆O的切线,C是切点,D是OB的延长线与CD的交点,CD∥AB,若CD=$\sqrt{5}$,则AC等于( )
如图,AB是半径为2的圆O的弦,CD是圆O的切线,C是切点,D是OB的延长线与CD的交点,CD∥AB,若CD=$\sqrt{5}$,则AC等于( )| A. | $\frac{\sqrt{6}}{3}$ | B. | $\frac{2\sqrt{6}}{3}$ | C. | 1 | D. | 2 |
9.若复数$\frac{a+i}{b-3i}$(a,b∈R)对应的点在虚轴上,则ab的值是( )
| A. | -15 | B. | 3 | C. | -3 | D. | 15 |