题目内容
4.求椭圆9x2+16y2=144的长轴和短轴的长、离心率、焦点和顶点的坐标.分析 将椭圆化成标准方程,算出a、b、c,再根据椭圆的基本概念,即可得到该椭圆的长轴长、短轴长、离心率、焦点和顶点坐标.
解答 解:椭圆方程化为$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{9}$=1,
∴a=4,b=3,c=$\sqrt{7}$,
∴长轴2a=8,短轴2b=6,
离心率e=$\frac{c}{a}$=$\frac{\sqrt{7}}{4}$,
焦点坐标(-$\sqrt{7}$,0)、($\sqrt{7}$,0),
顶点坐标(-4,0)(4,0)(0,3)(0,-3).
点评 本题给出椭圆的方程,求它的长轴长、短轴长、离心率、焦点和顶点坐标.着重考查了椭圆的标准方程与简单几何性质等知识,属于基础题.

练习册系列答案
相关题目
14.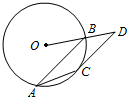 如图,AB是半径为2的圆O的弦,CD是圆O的切线,C是切点,D是OB的延长线与CD的交点,CD∥AB,若CD=$\sqrt{5}$,则AC等于( )
如图,AB是半径为2的圆O的弦,CD是圆O的切线,C是切点,D是OB的延长线与CD的交点,CD∥AB,若CD=$\sqrt{5}$,则AC等于( )
 如图,AB是半径为2的圆O的弦,CD是圆O的切线,C是切点,D是OB的延长线与CD的交点,CD∥AB,若CD=$\sqrt{5}$,则AC等于( )
如图,AB是半径为2的圆O的弦,CD是圆O的切线,C是切点,D是OB的延长线与CD的交点,CD∥AB,若CD=$\sqrt{5}$,则AC等于( )| A. | $\frac{\sqrt{6}}{3}$ | B. | $\frac{2\sqrt{6}}{3}$ | C. | 1 | D. | 2 |
9.若复数$\frac{a+i}{b-3i}$(a,b∈R)对应的点在虚轴上,则ab的值是( )
| A. | -15 | B. | 3 | C. | -3 | D. | 15 |
16.抛物线y=-$\frac{1}{8}{x^2}$的焦点坐标是( )
| A. | (0,$\frac{1}{32}$) | B. | ($\frac{1}{32}$,0) | C. | (0,-2) | D. | (-2,0) |
13.已知正三棱锥P-ABC,M和N分别为AB、PA的中点,MN⊥CN,若PA=1,则此正三棱锥的外接球表面积为( )
| A. | 5π | B. | 4π | C. | 3π | D. | 2π |