题目内容
【题目】为了响应教育部颁布的《关于推进中小学生研学旅行的意见》,某校计划开设八门研学旅行课程,并对全校学生的选择意向进行调查(调查要求全员参与,每个学生必须从八门课程中选出唯一一门课程).本次调查结果整理成条形图如下.图中,已知课程A,B,C,D,E为人文类课程,课程F,G,H为自然科学类课程.为进一步研究学生选课意向,结合图表,采取分层抽样方法从全校抽取1%的学生作为研究样本组(以下简称“组M”). 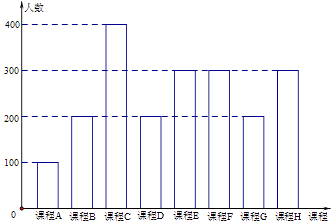
(Ⅰ)在“组M”中,选择人文类课程和自然科学类课程的人数各有多少?
(Ⅱ)为参加某地举办的自然科学营活动,从“组M”所有选择自然科学类课程的同学中随机抽取4名同学前往,其中选择课程F或课程H的同学参加本次活动,费用为每人1500元,选择课程G的同学参加,费用为每人2000元.
(ⅰ)设随机变量X表示选出的4名同学中选择课程G的人数,求随机变量X的分布列;
(ⅱ)设随机变量Y表示选出的4名同学参加科学营的费用总和,求随机变量Y的期望.
【答案】解:(Ⅰ)选择人文类课程的人数为(100+200+400+200+300)×1%=12(人);
选择自然科学类课程的人数为(300+200+300)×1%=8(人).
(Ⅱ)(ⅰ)依题意,随机变量X可取0,1,2. ![]() ;
; ![]() ;
; ![]() .
.
故随机变量X的分布列为
X | 0 | 1 | 2 |
p |
|
|
|
(ⅱ)法1:依题意,随机变量Y=2000X+1500(4﹣X)=6000+500X,
所以随机变量Y的数学期望为
E(Y)=6000+500E(X)
=6000+500( ![]() )
)
=6500.
(ⅱ)法2:依题意,随机变量Y可取6000,6500,7000.
所以随机变量Y的分布列为
Y | 6000 | 6500 | 7000 |
p |
|
|
|
所以随机变量Y的数学期望为
E(Y)= ![]() =6500
=6500
【解析】(Ⅰ)根据频率分布直方图的性质即可得出.(Ⅱ)(ⅰ)依题意,随机变量X可取0,1,2.利用“超几何分布列的计算公式与性质”即可得出.(ⅱ)法1:依题意,随机变量Y=2000X+1500(4﹣X),可得随机变量Y的数学期望为E(Y)=6000+500E(X).(ⅱ)法2:依题意,随机变量Y可取6000,6500,7000.求出随机变量Y的分布列,进而得出数学期望.
【考点精析】本题主要考查了离散型随机变量及其分布列的相关知识点,需要掌握在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列才能正确解答此题.

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案【题目】自2016年1月1日起,我国全面二孩政策正式实施,这次人口与生育政策的历史性调整,使得“要不要再生一个”“生二孩能休多久产假”等成为千千万万个家庭在生育决策上避不开的话题.为了解针对产假的不同安排方案形成的生育意愿,某调查机构随机抽取了200户有生育二胎能力的适龄家庭进行问卷调查,得到如下数据:
产假安排(单位:周) | 14 | 15 | 16 | 17 | 18 |
有生育意愿家庭数 | 4 | 8 | 16 | 20 | 26 |
(1)若用表中数据所得的频率代替概率,面对产假为14周与16周,估计某家庭有生育意愿的概率分别为多少?
(2)假设从5种不同安排方案中,随机抽取2种不同安排分别作为备选方案,然后由单位根据单位情况自主选择.
①求两种安排方案休假周数和不低于32周的概率;
②如果用ξ表示两种方案休假周数和.求随机变量ξ的分布及期望.