题目内容
【题目】如图1,在边长为2的菱形ABCD中,∠BAD=60°,将△BCD沿对角线BD折起到△B'CD的位置,使平面BC'D⊥平面ABD,E是BD的中点,FA⊥平面ABD,且FA=2 ![]() ,如图2.
,如图2. 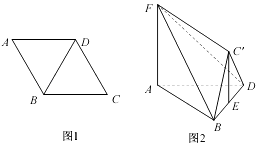
(1)求证:FA∥平面BC'D;
(2)求平面ABD与平面FBC'所成角的余弦值;
(3)在线段AD上是否存在一点M,使得C'M⊥平面FBC?若存在,求 ![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
【答案】
(1)证明:∵BC=CD,E为BD的中点,∴C′E⊥BD,
又平面BC'D⊥平面ABD,且平面BC'D∩平面ABD=BD,
∴C′E⊥ABD,
∵FA⊥平面ABD,∴FA∥C′E,而C′E平面BC'D,FA平面BC'D,
∴FA∥平面BC'D
(2)解:以DB所在直线为x轴,AE所在直线为y轴,EC′所在直线为z轴建立空间直角坐标系,
则B(1,0,0),A(0, ![]() ,0),D(﹣1,0,0),F(0,﹣
,0),D(﹣1,0,0),F(0,﹣ ![]() ,
, ![]() ),
),
C′(0,0, ![]() ),
),
∴ ![]() ,
, ![]() .
.
设平面FBC′的一个法向量为 ![]() ,
,
则 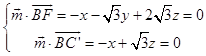 ,取z=1,则
,取z=1,则 ![]() .
.
又平面ABD的一个法向量为 ![]() .
.
∴cos< ![]() >=
>= ![]() =
= ![]() .
.
则平面ABD与平面FBC'所成角的余弦值为 ![]()

(3)解:线段AD上不存点M,使得C'M⊥平面FBC.
假设在线段AD上存在M(x,y,z),使得C'M⊥平面FBC,
设 ![]() ,则(x,y
,则(x,y ![]() ,z)=λ(﹣1,
,z)=λ(﹣1, ![]() ,0)=(﹣λ,
,0)=(﹣λ, ![]() ,0),
,0),
∴x=﹣λ,y= ![]() ,z=0.
,z=0.
则 ![]() =(﹣λ,
=(﹣λ, ![]() ,﹣
,﹣ ![]() ).
).
由 ![]() ,得
,得 ![]() ,即
,即 ![]() 错误.
错误.
∴线段AD上不存点M,使得C'M⊥平面FBC.
【解析】(1)由题意可得C′E⊥BD,又平面BC'D⊥平面ABD,且平面BC'D∩平面ABD=BD,再由面面垂直的性质可得C′E⊥ABD,结合已知可得FA∥C′E,由线面平行的判定可得FA∥平面BC'D;(2)以DB所在直线为x轴,AE所在直线为y轴,EC′所在直线为z轴建立空间直角坐标系,求出所用点的坐标,求得平面FBC′与平面ABD的一个法向量,由两法向量所成角的余弦值可得平面ABD与平面FBC'所成角的余弦值;(3)假设在线段AD上存在M(x,y,z),使得C'M⊥平面FBC,由 ![]() 求得M的坐标,得到
求得M的坐标,得到 ![]() ,由
,由 ![]() 加以判断.
加以判断.
【考点精析】认真审题,首先需要了解直线与平面平行的判定(平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行).

 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案