题目内容
19.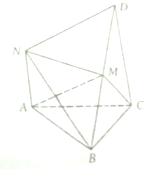 如图,在几何体NABCD中,CD⊥ABC.DC∥AN,CD=2AN=4,又AB=AC=BC=2,点M是BD上的动点(与B,D不重合)
如图,在几何体NABCD中,CD⊥ABC.DC∥AN,CD=2AN=4,又AB=AC=BC=2,点M是BD上的动点(与B,D不重合)(1)若M为BD的中点,求证:AM⊥BC;
(2)当直线MN与平面ACDN所成角为30°时,求二面角B-MC-A的正切值.
分析 (1)取BC的中点E,连结AE、AM、MC,利用中位线定理及线面平面的判定定理即得结论;
(2)以C为原点,建立空间直角坐标系,通过点M是BD上的动点,可得M(1-t,$\sqrt{3}$-$\sqrt{3}$t,4t),利用直线MN与平面ACDN所成角为30°可得$\overrightarrow{CM}$=($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$,2),则二面角B-MC-A的余弦值即为平面BMC的法向量与平面MCA的法向量的夹角的余弦值的绝对值,利用平方关系可知所求角的正弦值,进而可得结论.
解答 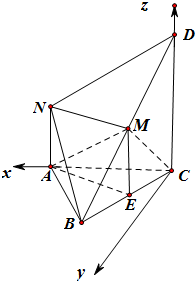 (1)证明:取BC的中点E,连结AE、AM、MC,
(1)证明:取BC的中点E,连结AE、AM、MC,
∵CD⊥平面ABC,DC∥AN,
∴AN⊥平面ABC,∴AN⊥BC,
又∵M为BD的中点,
∴ME∥CD∥AN,即ME⊥BC,
∵AB=AC=BC,E为BC中点,
∴AE⊥BC,
∴BC⊥平面AEM,
∴AM⊥BC;
(2)解:以C为原点,建立空间直角坐标系如图,
∵CD=2AN=4,又AB=AC=BC=2,
∴C(0,0,0),A(2,0,0),B(1,$\sqrt{3}$,0),
D(0,0,4),N(2,0,2),
则$\overrightarrow{CB}$=(1,$\sqrt{3}$,0),$\overrightarrow{CA}$=A(2,0,0),$\overrightarrow{BD}$=(-1,-$\sqrt{3}$,4),
设t$\overrightarrow{BD}$=$\overrightarrow{BM}$,则M(1-t,$\sqrt{3}$-$\sqrt{3}$t,4t),
∴$\overrightarrow{NM}$=(-1-t,$\sqrt{3}$-$\sqrt{3}$t,4t-2),$\overrightarrow{CM}$=(1-t,$\sqrt{3}$-$\sqrt{3}$t,4t),
∵直线MN与平面ACDN所成角为30°,
$\overrightarrow{m}$=(0,1,0)为平面ACDN的一个法向量,
∴$cos<\overrightarrow{m},\overrightarrow{NM}>$=$\frac{\sqrt{3}-\sqrt{3}t}{\sqrt{(1+t)^{2}+(\sqrt{3}-\sqrt{3}t)^{2}+(4t-2)^{2}}}$=cos60°,
解得t=$\frac{1}{2}$,即$\overrightarrow{CM}$=($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$,2),
设平面BMC的法向量为$\overrightarrow{p}$=(x,y,z),
由$\left\{\begin{array}{l}{\overrightarrow{p}•\overrightarrow{CB}=0}\\{\overrightarrow{p}•\overrightarrow{CM}=0}\end{array}\right.$,得$\left\{\begin{array}{l}{x+\sqrt{3}y=0}\\{\frac{1}{2}x+\frac{\sqrt{3}}{2}y+2z=0}\end{array}\right.$,
取y=-1,得$\overrightarrow{p}$=($\sqrt{3}$,-1,0),
设平面MCA的法向量为$\overrightarrow{q}$=(x,y,z),
由$\left\{\begin{array}{l}{\overrightarrow{q}•\overrightarrow{CM}=0}\\{\overrightarrow{q}•\overrightarrow{CA}=0}\end{array}\right.$,得$\left\{\begin{array}{l}{\frac{1}{2}x+\frac{\sqrt{3}}{2}y+2z=0}\\{2x=0}\end{array}\right.$,
取y=4,得$\overrightarrow{q}$=(0,4,-$\sqrt{3}$),
∴$cos<\overrightarrow{p},\overline{q}>$=$\frac{\overrightarrow{p}•\overrightarrow{q}}{|\overrightarrow{p}||\overrightarrow{q}|}$=$\frac{-4}{2×\sqrt{19}}$=-$\frac{2\sqrt{19}}{19}$,
∴二面角B-MC-A的余弦值为$\frac{2\sqrt{19}}{19}$,
由平方关系知其正弦值为$\sqrt{1-(\frac{2\sqrt{19}}{19})^{2}}$=$\frac{\sqrt{15×19}}{19}$,
∴二面角B-MC-A的正切值为$\frac{\frac{\sqrt{15×19}}{19}}{\frac{2\sqrt{19}}{19}}$=$\frac{\sqrt{15}}{2}$.
点评 本题考查线面垂直的判定定理,二面角的计算,数量积的运算,平方关系,注意解题方法的积累,属于难题.

| A. | {0} | B. | {1} | C. | {0,1} | D. | {1,2} |
| A. | 18种 | B. | 24种 | C. | 36种 | D. | 72种 |
经调查发现,堵车概率x在($\frac{2}{3}$,1)上变化,y在(0,$\frac{1}{2}$)上变化.
在不堵车的情况下.走线路甲需汽油费500元,走线路乙需汽油费545元.而每堵车1小时,需多花汽油费20元.路政局为了估计CD段平均堵车时间,调查了100名走甲线路的司机,得到表2数据.
| 堵车时间(单位:小时) | 频数 |
| [0,1] | 8 |
| (1,2] | 6 |
| (2,3] | 38 |
| (3,4] | 24 |
| (4,5] | 24 |
| (表2) | |
| CD段 | EF段 | GH段 | |
| 堵车概率 | x | y | $\frac{1}{4}$ |
| 平均堵车时间 (单位:小时) | a | 2 | 1 |
| (表1) | |||
(2)若只考虑所花汽油费期望值的大小,为了节约,求选择走甲线路的概率.
(3)在(2)的条件下,某4名司机中走甲线路的人数记为X,求X的数学期望.
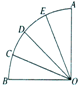 扇形AOB的半径为1,圆心角为90°,点C、D、E将弧AB分成四等分,连结OC、OD、OE,从图中所有的扇形中随机取出一个,面积恰好为$\frac{π}{8}$的概率是( )
扇形AOB的半径为1,圆心角为90°,点C、D、E将弧AB分成四等分,连结OC、OD、OE,从图中所有的扇形中随机取出一个,面积恰好为$\frac{π}{8}$的概率是( )| A. | $\frac{3}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{2}$ |
 如图,AB是圆O的直径,点C在圆O上,矩形DCBE所在的平面垂直于圆O所在的平面,AB=4,BE=1.
如图,AB是圆O的直径,点C在圆O上,矩形DCBE所在的平面垂直于圆O所在的平面,AB=4,BE=1. 如图,四棱锥P-ABCD,侧面PAD是边长为2的正三角形,且与底面垂直,底面ABCD是∠ABC=60°的菱形,M为PC的中点.
如图,四棱锥P-ABCD,侧面PAD是边长为2的正三角形,且与底面垂直,底面ABCD是∠ABC=60°的菱形,M为PC的中点.