题目内容
已知函数f(x)=x2-alnx(a∈R).
(1)若a=2,求f(x)的单调区间和极值;
(2)求f(x)在[1,e]上的最小值.
(1)若a=2,求f(x)的单调区间和极值;
(2)求f(x)在[1,e]上的最小值.
增区间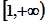 ;减区间
;减区间 ;
;

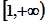 ;减区间
;减区间 ;
;

(1)当a=2时,解析式确定,利用导数求其增区间和极值即可.
(2)求导然后研究极值与区间端点值进行比较再确定函数f(x)的最小值,注意对参数a进行讨论
(2)求导然后研究极值与区间端点值进行比较再确定函数f(x)的最小值,注意对参数a进行讨论

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
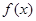 是定义在
是定义在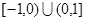 上的偶函数,当
上的偶函数,当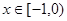 时,
时,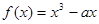 (
(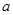 是实数)。
是实数)。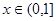 时,求f(x)的解析式;
时,求f(x)的解析式;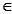 R,函数
R,函数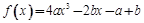 .
.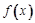 的最大值为|2a-b|﹢a;
的最大值为|2a-b|﹢a;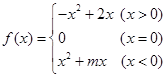 为奇函数,若函数
为奇函数,若函数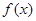 在区间
在区间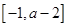 上单调递增,则
上单调递增,则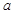 的取值范围是
的取值范围是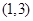
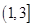
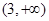
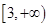
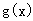 是
是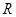 上的奇函数,且当
上的奇函数,且当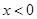 时
时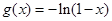 ,
,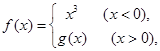 若
若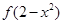 >
>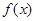 ,则实数
,则实数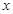 的取值范围是
的取值范围是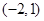
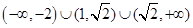
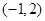
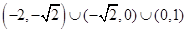
 函数
函数
 的单调区间;
的单调区间; 的取值范围.
的取值范围.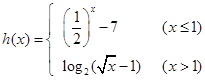
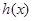 在区间
在区间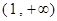 上的单调性并用定义证明;
上的单调性并用定义证明;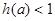 ,求
,求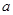 的取值范围.
的取值范围.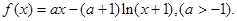
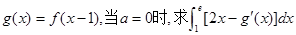 ;
;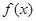 的单调区间;
的单调区间;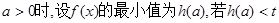 恒成立,求实数t的取值范围。
恒成立,求实数t的取值范围。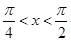 ,则函数
,则函数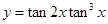 的最大值为 .
的最大值为 .