题目内容
【题目】已知:在平面四边形ABCD中,![]() ,
,![]() ,
,![]() ,
,![]() (如图1),若将
(如图1),若将![]() 沿对角线BD折叠,使
沿对角线BD折叠,使![]() (如图2).请在图2中解答下列问题.
(如图2).请在图2中解答下列问题.
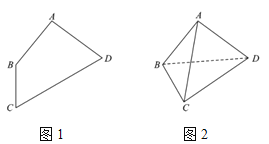
(1)证明:![]() ;
;
(2)求三棱锥![]() 的高.
的高.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)在图1中,根据平面几何知识可得BC=1且∠CBD=90°,在图2中可以得到AC2=AB2+CB2,从而可证明BC⊥平面ABD从而可证明结论.
(2)由(1)有![]() ,用等体积法有
,用等体积法有![]() .
.
证明:法1:由左图知,![]()
在△BDC中,∠CBD=135°-45°=90°,
∠BDC=75°-45°=30°,
![]() ,所以BC=1,
,所以BC=1,
又在右图中,因为AC![]() ,AB=AD
,AB=AD![]() ,所以AC2=AB2+CB2
,所以AC2=AB2+CB2
所以BC⊥AB
又因为∠CBD=90°,所以BC⊥平面ABD
所以BC⊥AD
法2:如右图,设BD的中点为O,连结A0,CO,因为∠A=90°,AB=AD![]()
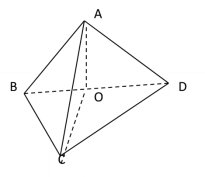
则![]()
由左图知,在△BDC中,∠CBD=135°-45°=90°
∠BDC=75°-45°=30°,所以BC=1,所以![]()
又因为AC![]() ,所以AC2=AO2+CO2
,所以AC2=AO2+CO2
所以AO⊥CO,所以AO⊥平面BCD,所以平面ABD⊥平面BCD,又∠CBD=90°
所以BC⊥平面ABD, 所以BC⊥AD
(2)因为AB=AD![]() ,AC
,AC![]() ,CD2=BC2+BD2=4
,CD2=BC2+BD2=4
所以CD2=AC2+AD2,所以AC⊥AD
设三棱锥B-ADC的高为h,则
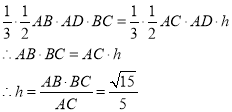

 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案【题目】某种产品的质量以其质量指标值来衡量,质量指标值越大表明质量越好,记其质量指标值为![]() ,当
,当![]() 时,产品为一级品;当
时,产品为一级品;当![]() 时,产品为二级品,当
时,产品为二级品,当![]() 时,产品为三级品,现用两种新配方(分别称为
时,产品为三级品,现用两种新配方(分别称为![]() 配方和
配方和![]() 配方)做实验,各生产了
配方)做实验,各生产了![]() 件这种产品,并测量了每件产品的质量指标值,得到下面的试验结果 :(以下均视频率为概率)
件这种产品,并测量了每件产品的质量指标值,得到下面的试验结果 :(以下均视频率为概率)
![]() 配方的频数分配表:
配方的频数分配表:
指标值分组 |
|
|
|
|
频数 |
|
|
|
|
![]() 配方的频数分配表:
配方的频数分配表:
指标值分组 |
|
|
|
|
|
频数 |
|
|
|
|
|
(1)若从![]() 配方产品中有放回地随机抽取
配方产品中有放回地随机抽取![]() 件,记“抽出的
件,记“抽出的![]() 配方产品中至少
配方产品中至少![]() 件二级品”为事件
件二级品”为事件![]() ,求事件
,求事件![]() 发生的概率
发生的概率![]() ;
;
(2)若两种新产品的利润率![]() 与质量指标
与质量指标![]() 满足如下关系:
满足如下关系: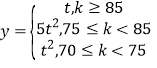 ,其中
,其中![]() ,从长期来看,投资哪种配方的产品平均利润率较大?
,从长期来看,投资哪种配方的产品平均利润率较大?