题目内容
【题目】动点![]() 与点
与点![]() 的距离和它到直线
的距离和它到直线![]() 的距离相等,记点
的距离相等,记点![]() 的轨迹为曲线
的轨迹为曲线![]()
(1)求曲线![]() 的方程
的方程
(2)设点![]() ,动点
,动点![]() 在曲线
在曲线![]() 上运动时,
上运动时,![]() 的最短距离为
的最短距离为![]() ,求
,求![]() 的值以及取到最小值时点
的值以及取到最小值时点![]() 的坐标
的坐标
(3)设![]() 为曲线
为曲线![]() 的任意两点,满足
的任意两点,满足![]() (
(![]() 为原点),试问直线
为原点),试问直线![]() 是否恒过一个定点?如果是,求出定点坐标;如果不是,说明理由
是否恒过一个定点?如果是,求出定点坐标;如果不是,说明理由
【答案】(1)![]() ;(2)
;(2)![]() ;
;![]() ;(3)恒过定点
;(3)恒过定点![]() ,理由见解析
,理由见解析
【解析】
(1)由抛物线定义可知轨迹为抛物线,结合焦点坐标求得曲线方程;
(2)设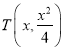 ,由两点间距离公式可得到
,由两点间距离公式可得到![]() ,结合二次函数的性质可知当
,结合二次函数的性质可知当![]() 时,
时,![]() 取得最小值,从而构造方程求得
取得最小值,从而构造方程求得![]() ;利用
;利用![]() 求得
求得![]() ,从而得到
,从而得到![]() 点坐标;
点坐标;
(3)将直线![]() 方程与抛物线方程联立可得
方程与抛物线方程联立可得![]() 坐标;由两点连线斜率公式求得直线
坐标;由两点连线斜率公式求得直线![]() 斜率,进而得到直线
斜率,进而得到直线![]() 的方程,整理可得恒过的定点坐标.
的方程,整理可得恒过的定点坐标.
(1)由抛物线定义可知,动点![]() 的轨迹是以
的轨迹是以![]() 为焦点,
为焦点,![]() 为准线的抛物线
为准线的抛物线
![]() 曲线
曲线![]() 的方程为:
的方程为:![]()
(2)设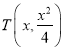

![]()
![]()
![]() 当
当![]() 时,
时,![]() ,解得:
,解得:![]()
此时![]()
![]()
(3)由题意知,直线![]() 斜率均存在且均不为零,可记为
斜率均存在且均不为零,可记为![]()
![]() ,与抛物线方程联立得:
,与抛物线方程联立得:![]()
![]()
同理可得:![]()
![]() 直线
直线![]() 斜率为
斜率为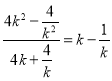
![]() 直线
直线![]() 方程为:
方程为:![]()
整理可得:![]()
![]() 当
当![]() ,
,![]() 时等式恒成立
时等式恒成立
![]() 直线
直线![]() 恒过点
恒过点![]()

练习册系列答案
相关题目
