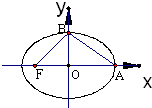
题目内容

若直线y=
3
2
x与椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)的交点在长轴上的射影恰好为椭圆的焦点，则椭圆的离心率是（　　）
A．
2
2
B．2C．
2
-1		D．
1
2
设直线y=
3
2
x与椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的交点为P，
则P的坐标为（c，
3c
2
），
∴
c2
a2
+
(
3c
2
)2
b2
=1，
∴4a4-17a2c2+4c4=0，
∴
c2
a2
=
1
4
或
c2
a2
=4（舍），
∴椭圆的离心率e=
c
a
=
1
2
．
故选D．
练习册系列答案
相关题目
如图，椭圆中心在坐标原点，F为左焦点，当
FB
⊥
AB
时，其离心率为
5
-1
2
，此类椭圆被称为“黄金椭圆”，类比“黄金椭圆”，可推算出“黄金双曲线”的离心率为（　　）
A．
5
+1
2
B．
5
-1
2
C．
5
+1		D．
5
-1
动点P为椭圆
x2
25
+
y2
16
=1上任意一点，左右焦点分别是F1，F2，直线l为∠F1PF2的外角平分线，过F1作直线l的垂线，垂足为Q，则点Q的轨迹方程是（　　）
A．x2+y2=25B．x2+y2=16C．x2-y2=25D．x22y2=16
已知P是椭圆上一点，F是椭圆的一个焦点，则以线段PF为直径的圆和以椭圆长轴为直径的圆的位置关系是（　　）
A．相离B．内切
C．内含D．可以内切，也可以内含
椭圆的长轴为A1A2，B为短轴一端点，若∠A1BA2=120°，则椭圆的离心率为（　　）
A．
6
3
B．
3
3
C．
3
2
D．
1
2
【文科】已知点A，B是椭圆
x2
m2
+
y2
n2
=1（m＞0，n＞0）上两点，且
AO
=λ
BO
，则λ=______．
椭圆2x2+3y2=6的焦距是（　　）
A．2(
3
-
2
)		B．2C．2
5
D．2(
3
+
2
)
已知椭圆的方程为
x2
9
+
y2
4
=1，则该椭圆的长半轴长为（　　）
A．3B．2C．6D．4
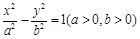已知F1、F2分别为双曲线的左、右焦点，点P为双曲线右支上的一点，满足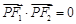，且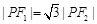，则该双曲线离心率为       ．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网