题目内容
动点P为椭圆
+
=1上任意一点,左右焦点分别是F1,F2,直线l为∠F1PF2的外角平分线,过F1作直线l的垂线,垂足为Q,则点Q的轨迹方程是( )
| x2 |
| 25 |
| y2 |
| 16 |
| A.x2+y2=25 | B.x2+y2=16 | C.x2-y2=25 | D.x22y2=16 |
由题意,P是以F1,F2为焦点的椭圆
+
=1上一点,
过焦点F2作∠F1PF2外角平分线的垂线,垂足为Q,
延长F2Q交F1P延长线于M,得PM=PF2,
由椭圆的定义知PF1+PF2=2a,
∴PF1+PM=MF1=2a,
连接OM,知OQ是三角形F1F2Q的中位线
∴OQ=a,即点Q到原点的距离是定值a,
由此知点Q的轨迹是以原点为圆心,以a为半径的圆,
∴点Q的轨迹方程是x2+y2=25.
故选:A.
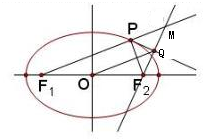
| x2 |
| 25 |
| y2 |
| 16 |
过焦点F2作∠F1PF2外角平分线的垂线,垂足为Q,
延长F2Q交F1P延长线于M,得PM=PF2,
由椭圆的定义知PF1+PF2=2a,
∴PF1+PM=MF1=2a,
连接OM,知OQ是三角形F1F2Q的中位线
∴OQ=a,即点Q到原点的距离是定值a,
由此知点Q的轨迹是以原点为圆心,以a为半径的圆,
∴点Q的轨迹方程是x2+y2=25.
故选:A.


练习册系列答案
相关题目