题目内容
直线y＝a与函数y＝x3－3x的图象有三个相异的交点，则a的取值范围为 ( )．
| A．(－2,2) | B．[－2,2] |
| C．[2，＋∞) | D．(－∞，－2] |
A
y′＝3x2－3，由y′＝0，得x＝1或x＝－1.
当x<－1时，y′>0；当－1<x<1时；当y′<0，当x>1时，y′>0.
所以y＝x3－3x在(－∞，－1)上递增，(－1,1)上递减，(1，＋∞)上递增．
当x＝－1时，y取得极大值(－1)3－3×(－1)＝2；
当x＝1时，y取得极小值13－3×1＝－2.
因此，a的取值范围为－2<a<2.
当x<－1时，y′>0；当－1<x<1时；当y′<0，当x>1时，y′>0.
所以y＝x3－3x在(－∞，－1)上递增，(－1,1)上递减，(1，＋∞)上递增．
当x＝－1时，y取得极大值(－1)3－3×(－1)＝2；
当x＝1时，y取得极小值13－3×1＝－2.
因此，a的取值范围为－2<a<2.
练习册系列答案
相关题目
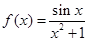．下列命题：（ ）
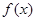的图象关于原点对称； ②函数
时,函数
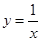的图象没有公共点，其中正确命题的序号是
＝3在区间(0，＋∞)上有且仅有一个解，那么实数a的取值范围为________．
的部分图象为（ ）