题目内容
【题目】已知f(x)是定义域为(0,+∞)的单调函数,若对任意的x∈(0,+∞),都有 ![]() ,且方程|f(x)﹣3|=x3﹣6x2+9x﹣4+a在区间(0,3]上有两解,则实数a的取值范围是( )
,且方程|f(x)﹣3|=x3﹣6x2+9x﹣4+a在区间(0,3]上有两解,则实数a的取值范围是( )
A.0<a≤5
B.a<5
C.0<a<5
D.a≥5
【答案】A
【解析】解:∵定义域为(0,+∞)的单调函数f(x) 满足f[f(x)+ ![]() x]=4,
x]=4,
∴必存在唯一的正实数a,
满足f(x)+ ![]() x=a,f(a)=4,①
x=a,f(a)=4,①
∴f(a)+ ![]() a=a,②
a=a,②
由①②得:4+ ![]() a=a,
a=a, ![]() a=a﹣4,
a=a﹣4,
a=( ![]() )a﹣4 , 左增,右减,有唯一解a=3,
)a﹣4 , 左增,右减,有唯一解a=3,
故f(x)+ ![]() x=a=3,
x=a=3,
f(x)=3﹣ ![]() x,
x,
由方程|f(x)﹣3|=x3﹣6x2+9x﹣4+a在区间(0,3]上有两解,
即有| ![]() x|=x3﹣6x2+9x﹣4+a,
x|=x3﹣6x2+9x﹣4+a,
由g(x)=x3﹣6x2+9x﹣4+a,g′(x)=3x2﹣12x+9=3(x﹣1)(x﹣3),
当1<x<3时,g′(x)<0,g(x)递减;当0<x<1时,g′(x)<0,g(x)递增.
g(x)在x=1处取得最大值a,g(0)=a﹣4,g(3)=a﹣4,
分别作出y=| ![]() x|,和y=x3﹣6x2+9x﹣4的图象,可得
x|,和y=x3﹣6x2+9x﹣4的图象,可得
两图象只有一个交点,将y=x3﹣6x2+9x﹣4的图象向上平移,
至经过点(3,1),有两个交点,
由g(3)=1即a﹣4=1,解得a=5,
当0<a≤5时,两图象有两个交点,
即方程|f(x)﹣3|=x3﹣6x2+9x﹣4+a在区间(0,3]上有两解.
故选:A.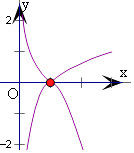
由题设知必存在唯一的正实数a,满足f(x)+ ![]() x=a,f(a)=4,f(a)+
x=a,f(a)=4,f(a)+ ![]() a=a,故4+
a=a,故4+ ![]() a=a,
a=a, ![]() a=a﹣4,a=(
a=a﹣4,a=( ![]() )a﹣4 , 左增,右减,有唯一解a=3,故f(x)+
)a﹣4 , 左增,右减,有唯一解a=3,故f(x)+ ![]() x=a=3,由题意可得|
x=a=3,由题意可得| ![]() x|=x3﹣6x2+9x﹣4+a在区间(0,3]上有两解,讨论g(x)=x3﹣6x2+9x﹣4+a的单调性和最值,分别画出作出y=|
x|=x3﹣6x2+9x﹣4+a在区间(0,3]上有两解,讨论g(x)=x3﹣6x2+9x﹣4+a的单调性和最值,分别画出作出y=| ![]() x|,和y=x3﹣6x2+9x﹣4的图象,通过平移即可得到a的范围.
x|,和y=x3﹣6x2+9x﹣4的图象,通过平移即可得到a的范围.

【题目】某险种的基本保费为![]() (单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:
(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:
上年度出险次数 | 0 | 1 | 2 | 3 | 4 |
|
保费 |
|
|
|
|
|
|
设该险种一续保人一年内出险次数与相应概率如下:
一年内出险次数 | 0 | 1 | 2 | 3 | 4 |
|
概率 | 0.30 | 0.15 | 0.20 | 0.20 | 0.10 | 0.05 |
(1)求一续保人本年度的保费高于基本保费的概率;
(2)已知一续保人本年度的保费高于基本保费,求其保费比基本保费高出![]() 的概率.
的概率.
