题目内容
8.已知圆C过两点A(0,4),B(4,6),且圆心在直线x-2y-2=0上.(1)求圆C的方程;
(2)若直线l过原点且被圆C截得的弦长为6,求直线l的方程.
分析 (1)线段AB的垂直平分线为2x+y-9=0与直线x-2y-2=0联立,求出圆心坐标,半径,即可求圆C的方程;
(2)分类讨论,求出圆心C到直线l的距离,利用直线l过原点且被圆C截得的弦长为6,结合勾股定理,求出k,即可求直线l的方程.
解答 解:(1)线段AB的垂直平分线为2x+y-9=0与直线x-2y-2=0联立
可得圆心C(4,1),…(3分)
∴半径r=5,
故所求圆C的标准方程为(x-4)2+(y-1)2=25.…(7分)
(2)当直线l的斜率不存在时,x=0显然满足题意; …(9分)
当直线l的斜率存在时,设直线l:y=kx,
∵弦长为6,∴圆心C到直线l的距离d=4,…(11分)
即$\frac{|4k-1|}{{\sqrt{{k^2}+1}}}=4$,解得$k=-\frac{15}{8}$,此时直线l:15x+8y=0,…(13分)
故所求直线l的方程为x=0或15x+8y=0.…(14分)
点评 本题考查了直线与圆的位置关系,涉及的知识有两点间的距离公式,点到直线的距离公式,圆的标准方程,属于中档题.

练习册系列答案
相关题目
20.已知集合M={x|x>$\frac{1}{x}$},N={x|y=$\frac{1}{\sqrt{1-lnx}}$},则M∩N=( )
| A. | (1,e) | B. | (0,1) | C. | (1,e] | D. | (e,+∞) |
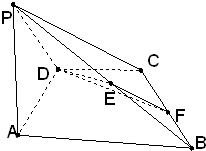 如图,四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为直角梯形,AD⊥DC,DC∥AB,PA=AB=2,AD=DC=1.
如图,四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为直角梯形,AD⊥DC,DC∥AB,PA=AB=2,AD=DC=1.