题目内容
3.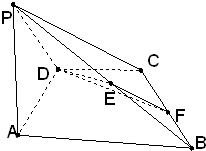 如图,四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为直角梯形,AD⊥DC,DC∥AB,PA=AB=2,AD=DC=1.
如图,四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为直角梯形,AD⊥DC,DC∥AB,PA=AB=2,AD=DC=1.(1)求证:PC⊥BC;
(2)E为PB中点,F为BC中点,求四棱锥D-EFCP的体积.
分析 (1)如图所示,利用线面垂直的性质定理可得:PA⊥BC,由AB2=AC2+BC2,可得BC⊥AC,再利用线面垂直的判定定理即可证明.
(2)由于S四边形PEFC=$\frac{3}{4}{S}_{△PBC}$,可得VD-PEFC=$\frac{3}{4}{V}_{D-PBC}$=$\frac{3}{4}{V}_{P-BCD}$=$\frac{3}{4}×\frac{1}{3}PA×{S}_{△BCD}$,即可得出.
解答 (1)证明:如图所示,
∵PA⊥平面ABCD,BC?平面ABCD,
∴PA⊥BC,
连接AC,∵AD=CD,AD⊥CD,
∴AC=$\sqrt{2}$,
由余弦定理可得:BC2=AC2+AB2-2AC•ABcos45°=2,
∴BC=$\sqrt{2}$,又AB=2,
∴AB2=AC2+BC2,
∴BC⊥AC,
∴BC⊥平面PAC,又PC?平面PAC,
∴PC⊥BC.
(2)解:S四边形PEFC=$\frac{3}{4}{S}_{△PBC}$,
∴VD-PEFC=$\frac{3}{4}{V}_{D-PBC}$=$\frac{3}{4}{V}_{P-BCD}$=$\frac{3}{4}×\frac{1}{3}PA×{S}_{△BCD}$=$\frac{1}{4}×2$×$\frac{1}{2}×{1}^{2}$=$\frac{1}{4}$.
点评 本题考查了线面垂直的判定与性质定理、余弦定理、三棱锥的体积计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
11.设函数f(x)=3x2-1,则f(a)-f(-a)的值是( )
| A. | 0 | B. | 3a2-1 | C. | 6a2-2 | D. | 6a2 |
12.设O是边长为1的等边△ABC的内心,则$\overrightarrow{OA}$$•\overrightarrow{OB}$=( )
| A. | $\frac{1}{6}$ | B. | -$\frac{1}{6}$ | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
 已知在△ABC中,A、B、C对边分别为a、b、c,已知b=2$\sqrt{7}$,B=60°,a+c=10.
已知在△ABC中,A、B、C对边分别为a、b、c,已知b=2$\sqrt{7}$,B=60°,a+c=10.