题目内容
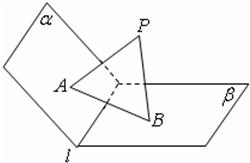
如图,在三棱锥P-ABC中,E,F分别为AC,BC的中点.
(1)求证:EF∥平面PAB;
(2)若平面PAC⊥平面ABC,且PA=PC,∠ABC=90°,求证:平面PEF⊥平面PBC.
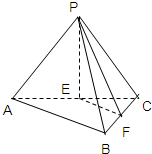
(1)求证:EF∥平面PAB;
(2)若平面PAC⊥平面ABC,且PA=PC,∠ABC=90°,求证:平面PEF⊥平面PBC.

(本小题满分14分)
证明:(1)∵E,F分别是AC,BC的中点,∴EF∥AB.---(1分)
又EF?平面PAB,-----(2分)
AB?平面PAB,------(3分)
∴EF∥平面PAB.-----(4分)
(2)在三角形PAC中,∵PA=PC,E为AC中点,
∴PE⊥AC.-----(5分)
∵平面PAC⊥平面ABC,
平面PAC∩平面ABC=AC,
∴PE⊥平面ABC.-----(7分)
∴PE⊥BC.-----(8分)
又EF∥AB,∠ABC=90°,∴EF⊥BC,------(10分)
又EF∩PE=E,
∴BC⊥平面PEF.------(12分)
∴平面PEF⊥平面PBC.----(14分)
证明:(1)∵E,F分别是AC,BC的中点,∴EF∥AB.---(1分)
又EF?平面PAB,-----(2分)
AB?平面PAB,------(3分)
∴EF∥平面PAB.-----(4分)
(2)在三角形PAC中,∵PA=PC,E为AC中点,
∴PE⊥AC.-----(5分)

∵平面PAC⊥平面ABC,
平面PAC∩平面ABC=AC,
∴PE⊥平面ABC.-----(7分)
∴PE⊥BC.-----(8分)
又EF∥AB,∠ABC=90°,∴EF⊥BC,------(10分)
又EF∩PE=E,
∴BC⊥平面PEF.------(12分)
∴平面PEF⊥平面PBC.----(14分)

练习册系列答案
相关题目
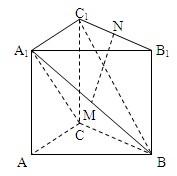
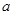 的正方体
的正方体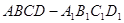 中,
中,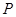 为
为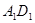 的中点,
的中点,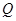 为
为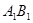 上任意一点,
上任意一点, 为
为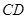 上两点,且
上两点,且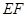 的长为定值,则下面四个值中不是定值的是( )
的长为定值,则下面四个值中不是定值的是( )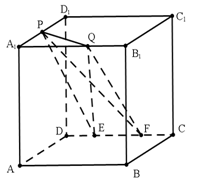
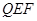 的距离
的距离 与平面
与平面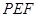 所成的角
所成的角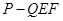 的体积
的体积 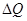
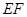 的面积
的面积