题目内容
【题目】已知![]() ,
, ![]() .
.
(1)若![]() 为真命题,求实数
为真命题,求实数![]() 的取值范围;
的取值范围;
(2)若![]() 是
是![]() 成立的充分不必要条件,求实数
成立的充分不必要条件,求实数![]() 的取值范围.
的取值范围.
【答案】:(1)-2≤x≤8.(2)m≥6.
【解析】试题分析:
(1)求解一元二次不等式可得p为真命题时实数x的取值范围是-2≤x≤8;
(2)结合(1)的结论得到关于实数m的不等式组,求解不等式组可得实数m的取值范围是m≥6.
试题解析:
(1)由-x2+6x+16≥0,解得-2≤x≤8;
所以当p为真命题时,实数x的取值范围为-2≤x≤8.
(2)解法一:若q为真,可由x2-4x+4-m2≤0(m>0),解得2-m≤x≤2+m(m>0).
若p是q成立的充分不必要条件,则[-2,8]是[2-m,2+m]的真子集,
所以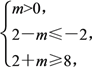 (两等号不同时成立),得m≥6.
(两等号不同时成立),得m≥6.
所以实数m的取值范围是m≥6.
解法二:设f(x)=x2-4x+4-m2(m>0),
若p是q成立的充分不必要条件,
∵x2-4x+4-m2≤0在[-2,8]恒成立,
则有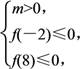 (两等号不同时成立),解得m≥6.
(两等号不同时成立),解得m≥6.

练习册系列答案
相关题目