题目内容
已知四棱锥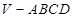 的底面ABCD是边长为
的底面ABCD是边长为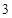 的正方形,侧棱
的正方形,侧棱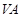 与底面垂直,若异面直线AC与VD所成的角为
与底面垂直,若异面直线AC与VD所成的角为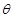 ,且
,且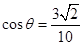 ,则四棱锥
,则四棱锥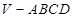 的体积为
的体积为
____________.
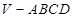 的底面ABCD是边长为
的底面ABCD是边长为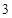 的正方形,侧棱
的正方形,侧棱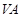 与底面垂直,若异面直线AC与VD所成的角为
与底面垂直,若异面直线AC与VD所成的角为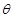 ,且
,且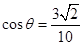 ,则四棱锥
,则四棱锥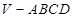 的体积为
的体积为____________.
12
略

练习册系列答案
相关题目
题目内容
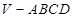 的底面ABCD是边长为
的底面ABCD是边长为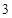 的正方形,侧棱
的正方形,侧棱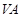 与底面垂直,若异面直线AC与VD所成的角为
与底面垂直,若异面直线AC与VD所成的角为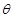 ,且
,且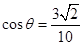 ,则四棱锥
,则四棱锥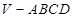 的体积为
的体积为