题目内容
(12分)如图所示,以AB=4 cm,BC=3 cm的长方形ABCD为底面的长方体被平面斜着截断的几何体,EFGH是它的截面.当AE=5 cm,BF=8 cm,CG=12 cm时,试回答下列问题:
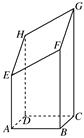
(1)求DH的长;
(2)求这个几何体的体积;
(3)截面四边形EFGH是什么图形?证明你的结论.

(1)求DH的长;
(2)求这个几何体的体积;
(3)截面四边形EFGH是什么图形?证明你的结论.
解:(1)过E作EB1⊥BF,垂足为B1,则BB1=AE=5(cm),
所以B1F=8-5=3(cm).
因为平面ABFE∥平面DCGH,EF和HG是它们分别与截面的交线,所以EF∥HG.
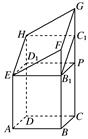
过H作HC1⊥CG,垂足为C1,
则GC1=FB1=3(cm),
DH=12-3=9(cm). ----------------------------------- 4分
(2)作ED1⊥DH,垂足为D1,B1P⊥CG,垂足为P,连结D1P,B1C1,则几何体被分割成一个长方体ABCD-EB1PD1,一个斜三棱柱EFB1-HGC1,一个直三棱柱EHD1-B1C1P.从而几何体的体积为
V=3×4×5+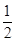 ×3×4×3+
×3×4×3+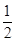 ×3×4×4=102(cm3).--------------8分
×3×4×4=102(cm3).--------------8分
(3)是菱形.
证明:由(1)知EF∥HG,同理EH∥FG.于是EFGH是平行四边形.
因为EF=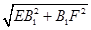 =
=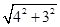
=5(cm),
DD1=AE=5(cm),ED1=AD=3(cm),
HD1=4(cm),
所以EH=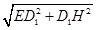 =
=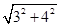
=5(cm).
所以EF=EH.
故EFGH是菱形. ------------------------------------------12分
所以B1F=8-5=3(cm).
因为平面ABFE∥平面DCGH,EF和HG是它们分别与截面的交线,所以EF∥HG.

过H作HC1⊥CG,垂足为C1,
则GC1=FB1=3(cm),
DH=12-3=9(cm). ----------------------------------- 4分
(2)作ED1⊥DH,垂足为D1,B1P⊥CG,垂足为P,连结D1P,B1C1,则几何体被分割成一个长方体ABCD-EB1PD1,一个斜三棱柱EFB1-HGC1,一个直三棱柱EHD1-B1C1P.从而几何体的体积为
V=3×4×5+
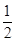 ×3×4×3+
×3×4×3+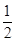 ×3×4×4=102(cm3).--------------8分
×3×4×4=102(cm3).--------------8分(3)是菱形.
证明:由(1)知EF∥HG,同理EH∥FG.于是EFGH是平行四边形.
因为EF=
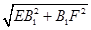 =
=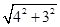
=5(cm),
DD1=AE=5(cm),ED1=AD=3(cm),
HD1=4(cm),
所以EH=
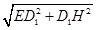 =
=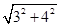
=5(cm).
所以EF=EH.
故EFGH是菱形. ------------------------------------------12分
略

练习册系列答案
相关题目
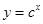 在R上单调递减;q:不等式
在R上单调递减;q:不等式
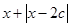 >1的解集为R,如果“p或q”为真,且“p且q”为假,求c的取值范围。
>1的解集为R,如果“p或q”为真,且“p且q”为假,求c的取值范围。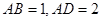 ,
,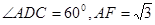 .
.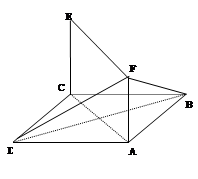
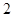 的正方形
的正方形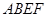 中,
中,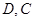 分别为
分别为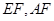 上的点,且
上的点,且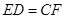 ,现沿
,现沿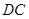 把
把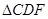 剪切、拼接成如图(2)的图形,再将
剪切、拼接成如图(2)的图形,再将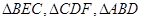 沿
沿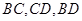 折起,使
折起,使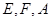 三点重合于点
三点重合于点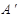 。
。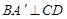 ;
;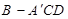 体积的最大值。
体积的最大值。
 中,平面
中,平面 平面
平面 .底面
.底面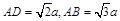 ,
,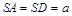 .(Ⅰ)求证:
.(Ⅰ)求证: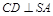 ;
; 的大小.
的大小.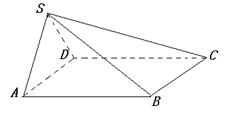
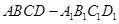 中,棱长是1,
中,棱长是1,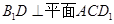 ;
;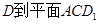 的距离。
的距离。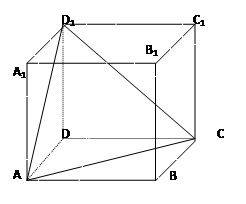
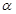 内的两条直线垂直,则
内的两条直线垂直,则 .
.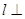 平面
平面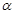 ,直线
,直线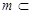 平面
平面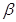 ,下面三个说法:
,下面三个说法: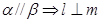 ;②
;②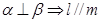 ;③
;③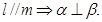
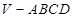 的底面ABCD是边长为
的底面ABCD是边长为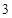 的正方形,侧棱
的正方形,侧棱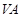 与底面垂直,若异面直线AC与VD所成的角为
与底面垂直,若异面直线AC与VD所成的角为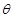 ,且
,且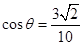 ,则四棱锥
,则四棱锥