题目内容
.(本题满分12分)
如图,ABCD是菱形,PA⊥平面ABCD,PA=AD=2,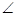 BAD=60°.
BAD=60°.
(1)证明:面PBD⊥面PAC;
(2)求锐二面角A—PC—B的余弦值.
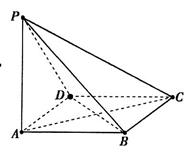
如图,ABCD是菱形,PA⊥平面ABCD,PA=AD=2,
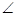 BAD=60°.
BAD=60°.(1)证明:面PBD⊥面PAC;
(2)求锐二面角A—PC—B的余弦值.

1)因为四边形ABCD是菱形,
所以AC
因为PA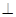 平面ABCD,
平面ABCD,
所有PA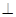 BD.…………………………2分
BD.…………………………2分
又因为PA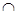 AC=A,
AC=A,
所以BD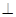 面 PAC.……………………3分
面 PAC.……………………3分
而BD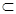 面PBD,
面PBD,
所以面PBD 面PAC.…………………5分
面PAC.…………………5分
(2)如图,设AC BD=O.取PC的中点Q,连接OQ.
BD=O.取PC的中点Q,连接OQ.
在△APC中,AO=OC,CQ=QP,OQ为△APC的中位线,所以OQ//PA.
因为PA 平面ABCD,
平面ABCD,
所以OQ 平面ABCD,……………………………………………………6分
平面ABCD,……………………………………………………6分
以OA、OB、OQ所在直线分别为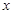 轴、
轴、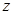 轴,建立空间直角坐标系O
轴,建立空间直角坐标系O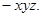
则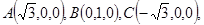
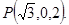 ………………………………………………………………………7分
………………………………………………………………………7分
因为BO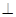 面PAC,
面PAC,
所以平面PAC的一个法向量为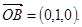 …………………………………8分
…………………………………8分
设平面PBC的一个法向量为

而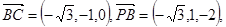
由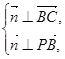 得
得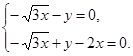
令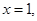 则
则
所以 为平面PBC的一个法向量.……………………………10分
为平面PBC的一个法向量.……………………………10分
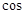 <
<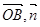 >
>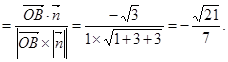 ……………………12分
……………………12分
所以AC

因为PA
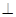 平面ABCD,
平面ABCD,所有PA
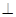 BD.…………………………2分
BD.…………………………2分又因为PA
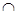 AC=A,
AC=A,所以BD
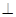 面 PAC.……………………3分
面 PAC.……………………3分而BD
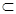 面PBD,
面PBD,所以面PBD
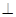 面PAC.…………………5分
面PAC.…………………5分(2)如图,设AC
 BD=O.取PC的中点Q,连接OQ.
BD=O.取PC的中点Q,连接OQ.在△APC中,AO=OC,CQ=QP,OQ为△APC的中位线,所以OQ//PA.
因为PA
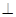 平面ABCD,
平面ABCD,所以OQ
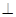 平面ABCD,……………………………………………………6分
平面ABCD,……………………………………………………6分以OA、OB、OQ所在直线分别为
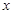 轴、
轴、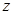 轴,建立空间直角坐标系O
轴,建立空间直角坐标系O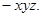
则
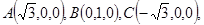
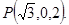 ………………………………………………………………………7分
………………………………………………………………………7分因为BO
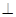 面PAC,
面PAC,所以平面PAC的一个法向量为
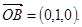 …………………………………8分
…………………………………8分设平面PBC的一个法向量为


而
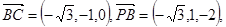
由
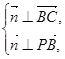 得
得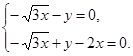
令
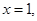 则
则
所以
 为平面PBC的一个法向量.……………………………10分
为平面PBC的一个法向量.……………………………10分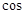 <
<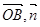 >
>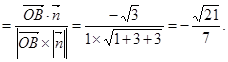 ……………………12分
……………………12分略

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 、
、 、
、 ,若
,若


 ∥平面
∥平面 ,
, ,那么过点
,那么过点 且平行于
且平行于 内
内
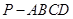 的底面为直角梯形,
的底面为直角梯形, ,
, 底面
底面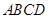 ,且
,且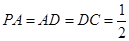 ,
,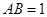 ,
,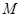 是
是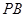 的中点。
的中点。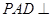 面
面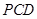 ;
;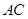 与
与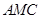 与面
与面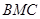 所成二面角的余弦值。
所成二面角的余弦值。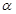 内的两条直线垂直,则
内的两条直线垂直,则 .
.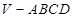 的底面ABCD是边长为
的底面ABCD是边长为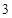 的正方形,侧棱
的正方形,侧棱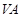 与底面垂直,若异面直线AC与VD所成的角为
与底面垂直,若异面直线AC与VD所成的角为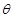 ,且
,且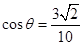 ,则四棱锥
,则四棱锥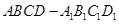 的棱长为
的棱长为 ,则点
,则点 到
到 的距离为_____________.
的距离为_____________. 