题目内容
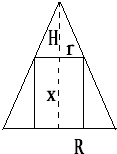 已知一个圆锥的底面半径为R,高为H,在其中有一个高为x的内接圆柱,
已知一个圆锥的底面半径为R,高为H,在其中有一个高为x的内接圆柱,(1)求此圆柱的侧面积表达式;
(2)x为何值时,圆柱的侧面积最大?
分析:(1)由题意,圆柱的高已知为x,故求出圆柱底面的半径r关于x的表达式,再由公式求出侧面积的表达式,由图知,求底面半径可利用过轴的截面建立比例关系
=
,从中解出底面半径表达式;
(2)由(1)S圆柱侧面=2πRx-
x2,此是一个关于圆柱高的二次函数,由二次函数的知识判断出函数的最值,即可得到圆柱侧面积的最大值,同时求出此时的x的值
| r |
| R |
| H-x |
| H |
(2)由(1)S圆柱侧面=2πRx-
| 2πR |
| H |
解答: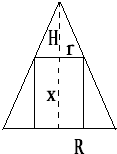 解:(1)过圆锥及内接的圆柱的轴作截面,如图:
解:(1)过圆锥及内接的圆柱的轴作截面,如图:
因为
=
,所以r=R-
x,
从而S圆柱侧面=2πrx=2πRx-
x2.
(2)由(1)S圆柱侧面=2πRx-
x2
因为-
<0,
所以当x=-
=
=
时,S侧最大,
从而当x=
,即圆柱的高为圆锥高的一半时,圆柱的侧面积最大.
 解:(1)过圆锥及内接的圆柱的轴作截面,如图:
解:(1)过圆锥及内接的圆柱的轴作截面,如图:因为
| r |
| R |
| H-x |
| H |
| R |
| H |
从而S圆柱侧面=2πrx=2πRx-
| 2πR |
| H |
(2)由(1)S圆柱侧面=2πRx-
| 2πR |
| H |
因为-
| 2πR |
| H |
所以当x=-
| b |
| 2a |
| 2πR | ||
|
| H |
| 2 |
从而当x=
| H |
| 2 |
点评:本题是一个旋转体中的最值问题,解题的关键是建立起圆柱侧面积的函数关系,利用函数的最值求侧面积的最值,本题的难点是作出旋转体的轴截面,由此截面上的比例关系将底面半径用高表示出来,从而由公式建立起侧面积关于高x的函数关系,这也是本题的重点,本题考查了数形结合的思想,函数的思想,利用函数求最值是函数的一个重要运用,

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
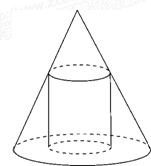 已知一个圆锥的底面半径为R,高为H,在其中有一个高为x的内接圆柱. 如图所示.
已知一个圆锥的底面半径为R,高为H,在其中有一个高为x的内接圆柱. 如图所示. 如图,已知一个圆锥的底面半径为R,高为h,在其中有一个高为x的内接圆柱(其中R,h均为常数).
如图,已知一个圆锥的底面半径为R,高为h,在其中有一个高为x的内接圆柱(其中R,h均为常数). 如图,已知一个圆锥的底面半径为R=1,高为h=2.,一个圆柱的下底面在圆锥的底面上,且圆柱的上底面为圆锥的截面,设圆柱的高为x.
如图,已知一个圆锥的底面半径为R=1,高为h=2.,一个圆柱的下底面在圆锥的底面上,且圆柱的上底面为圆锥的截面,设圆柱的高为x.