题目内容
已知一个圆锥的底面半径为R,高为h,在圆锥内部有一个高为x的内接圆柱.
(1)画出圆锥及其内接圆柱的轴截面;
(2)求圆柱的侧面积;
(3)当x为何值时,圆柱的侧面积最大?
(1)画出圆锥及其内接圆柱的轴截面;
(2)求圆柱的侧面积;
(3)当x为何值时,圆柱的侧面积最大?
分析:(1)由题设条件能画出圆锥及其内接圆柱的轴截面.
(2)设所求的圆柱的底面半径为r.它的侧面积S=2πrx,由
=
,能求出圆柱的侧面积.
(3)由圆柱的侧面积S是关于x的二次函数S=-
x2+2πRx,能推导出当圆柱的高是已知圆锥的一半时,它的侧面积最大.
(2)设所求的圆柱的底面半径为r.它的侧面积S=2πrx,由
| r |
| R |
| h-x |
| h |
(3)由圆柱的侧面积S是关于x的二次函数S=-
| 2πR |
| h |
解答: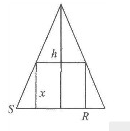 解:(1)圆锥及其内接圆柱的轴截面如图所示.
解:(1)圆锥及其内接圆柱的轴截面如图所示.
(2)设所求的圆柱的底面半径为r.它的侧面积S=2πrx,
∵
=
,∴r=R-
•x,
∴S=2πRx-
x2.
(3)由(2)知圆柱的侧面积S是关于x的二次函数:
S=-
x2+2πRx,
∵S的表达式中x2的系数小于0,
∴这个二次函数有最大值,
这时圆柱的高x=-
=
,
即当圆柱的高是已知圆锥的一半时,它的侧面积最大.
 解:(1)圆锥及其内接圆柱的轴截面如图所示.
解:(1)圆锥及其内接圆柱的轴截面如图所示.(2)设所求的圆柱的底面半径为r.它的侧面积S=2πrx,
∵
| r |
| R |
| h-x |
| h |
| R |
| h |
∴S=2πRx-
| 2πR |
| h |
(3)由(2)知圆柱的侧面积S是关于x的二次函数:
S=-
| 2πR |
| h |
∵S的表达式中x2的系数小于0,
∴这个二次函数有最大值,
这时圆柱的高x=-
| 2πR | ||
-2•
|
| h |
| 2 |
即当圆柱的高是已知圆锥的一半时,它的侧面积最大.
点评:本题考查圆锥及其内接圆柱的轴截面的画法,考查圆柱的侧面积的求法,考查圆柱的侧面积的最大值的求法,解题时要认真审题,注意等价转化思想的合理运用.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
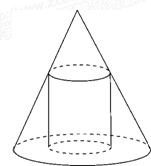 已知一个圆锥的底面半径为R,高为H,在其中有一个高为x的内接圆柱. 如图所示.
已知一个圆锥的底面半径为R,高为H,在其中有一个高为x的内接圆柱. 如图所示. 如图,已知一个圆锥的底面半径为R,高为h,在其中有一个高为x的内接圆柱(其中R,h均为常数).
如图,已知一个圆锥的底面半径为R,高为h,在其中有一个高为x的内接圆柱(其中R,h均为常数). 如图,已知一个圆锥的底面半径为R=1,高为h=2.,一个圆柱的下底面在圆锥的底面上,且圆柱的上底面为圆锥的截面,设圆柱的高为x.
如图,已知一个圆锥的底面半径为R=1,高为h=2.,一个圆柱的下底面在圆锥的底面上,且圆柱的上底面为圆锥的截面,设圆柱的高为x.