题目内容
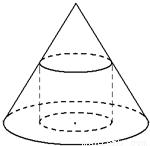
 如图,已知一个圆锥的底面半径为R=1,高为h=2.,一个圆柱的下底面在圆锥的底面上,且圆柱的上底面为圆锥的截面,设圆柱的高为x.
如图,已知一个圆锥的底面半径为R=1,高为h=2.,一个圆柱的下底面在圆锥的底面上,且圆柱的上底面为圆锥的截面,设圆柱的高为x.(1)求圆柱的侧面积.
(2)x为何值时,圆柱的侧面积最大?
分析:(1)根据已知中圆锥的底面半径为R=1,高为h=2,圆柱的高为x,根据相似三角形的性质,分析圆锥的高与底面半径的关系,可得圆柱的侧面积.
(2)由(1)中圆柱侧面积的表达式,结合二次函数的图象和性质,可得答案.
(2)由(1)中圆柱侧面积的表达式,结合二次函数的图象和性质,可得答案.
解答: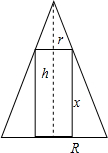 解:(1)作轴截面如图所示,
解:(1)作轴截面如图所示,
设内接圆柱底面半径为r
由三角形相似得
=
,
所以r=
(2-x),
S圆柱侧=2πx•
(2-x)=πx(2-x)=π(-x2+2x)(0<x<2).…(8分)
(2)S圆柱侧=π(-x2+2x)=π[-(x-1)2+1],又0<x<2,
所以当x=1时,S圆柱侧最大=π.…(12分)
 解:(1)作轴截面如图所示,
解:(1)作轴截面如图所示,设内接圆柱底面半径为r
由三角形相似得
| r |
| R |
| h-x |
| h |
所以r=
| 1 |
| 2 |
S圆柱侧=2πx•
| 1 |
| 2 |
(2)S圆柱侧=π(-x2+2x)=π[-(x-1)2+1],又0<x<2,
所以当x=1时,S圆柱侧最大=π.…(12分)
点评:本题考查的知识点是圆柱的表面积,二次函数的图象和性质,熟练掌握二次函数的图象和性质是解答的关键.

练习册系列答案
相关题目
 如图,已知一个圆锥的底面半径为R,高为h,在其中有一个高为x的内接圆柱(其中R,h均为常数).
如图,已知一个圆锥的底面半径为R,高为h,在其中有一个高为x的内接圆柱(其中R,h均为常数). 用铁皮制作一个无盖的圆锥形容器,如图,已知该圆锥的母线与底面所在平面的夹角为45°,容器的高为10cm.制作该容器需要多少面积的铁皮?该容器的容积又是多少?(衔接部分忽略不计,结果精确到0.1cm2)
用铁皮制作一个无盖的圆锥形容器,如图,已知该圆锥的母线与底面所在平面的夹角为45°,容器的高为10cm.制作该容器需要多少面积的铁皮?该容器的容积又是多少?(衔接部分忽略不计,结果精确到0.1cm2)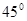 ,容器的高为
,容器的高为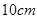 .制作该容器需要多少面积的铁皮?该容器的容积又是多少?(衔接部分忽略不计,结果精确到
.制作该容器需要多少面积的铁皮?该容器的容积又是多少?(衔接部分忽略不计,结果精确到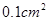 )
)
 h时,求内接圆柱上方的圆锥的体积V;
h时,求内接圆柱上方的圆锥的体积V;