题目内容
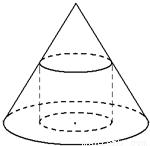
 如图,已知一个圆锥的底面半径为R,高为h,在其中有一个高为x的内接圆柱(其中R,h均为常数).
如图,已知一个圆锥的底面半径为R,高为h,在其中有一个高为x的内接圆柱(其中R,h均为常数).(1)当x=
| 2 | 3 |
(2)当x为何值时,这个内接圆柱的侧面积最大?并求出其最大值.
分析:(1)根据圆锥的底面半径与高,可得内接圆柱的高为x时,它的高h,由此结合圆柱体积公式即可列出用x表示圆柱的体积的式子;
(2)由(1)可得圆柱的侧面积S=2π•
(h-x)x,结合二次函数的单调性与最值,可得当圆柱的底面半径为1时,圆柱的侧面积最大,侧面积有最大值为6π.
(2)由(1)可得圆柱的侧面积S=2π•
| h |
| R |
解答: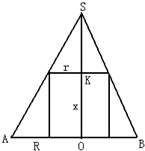 解:圆锥、圆柱的轴截面如图所示,其中SO=h,OA=OB=R,OK=x.
解:圆锥、圆柱的轴截面如图所示,其中SO=h,OA=OB=R,OK=x.
设圆柱底面半径为r,则
=
(3分)
(1)当x=
h时,r=
R,SK=
h
∴V=
•πr2•SK=
•
πR2•
h=
πhR2
(2)设圆柱的侧面积为S.
∵r=
(h-x),
∴S=2π•
(h-x)x=-
(x-
)2+
∴当x=
时,Smax=
.
 解:圆锥、圆柱的轴截面如图所示,其中SO=h,OA=OB=R,OK=x.
解:圆锥、圆柱的轴截面如图所示,其中SO=h,OA=OB=R,OK=x.设圆柱底面半径为r,则
| r |
| R |
| h-x |
| h |
(1)当x=
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
∴V=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 9 |
| 1 |
| 3 |
| 1 |
| 81 |
(2)设圆柱的侧面积为S.
∵r=
| h |
| R |
∴S=2π•
| h |
| R |
| 2πR |
| h |
| h |
| 2 |
| πRh |
| 2 |
∴当x=
| h |
| 2 |
| πRh |
| 2 |
点评:本题给出特殊圆锥,求它的内接圆锥的侧面积的最大值,着重考查了圆柱的体积、侧面积公式和旋转体的内接外切等知识点

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
 如图,已知一个圆锥的底面半径为R=1,高为h=2.,一个圆柱的下底面在圆锥的底面上,且圆柱的上底面为圆锥的截面,设圆柱的高为x.
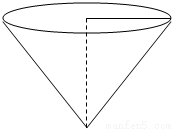
如图,已知一个圆锥的底面半径为R=1,高为h=2.,一个圆柱的下底面在圆锥的底面上,且圆柱的上底面为圆锥的截面,设圆柱的高为x. 用铁皮制作一个无盖的圆锥形容器,如图,已知该圆锥的母线与底面所在平面的夹角为45°,容器的高为10cm.制作该容器需要多少面积的铁皮?该容器的容积又是多少?(衔接部分忽略不计,结果精确到0.1cm2)
用铁皮制作一个无盖的圆锥形容器,如图,已知该圆锥的母线与底面所在平面的夹角为45°,容器的高为10cm.制作该容器需要多少面积的铁皮?该容器的容积又是多少?(衔接部分忽略不计,结果精确到0.1cm2)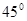 ,容器的高为
,容器的高为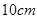 .制作该容器需要多少面积的铁皮?该容器的容积又是多少?(衔接部分忽略不计,结果精确到
.制作该容器需要多少面积的铁皮?该容器的容积又是多少?(衔接部分忽略不计,结果精确到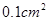 )
)
 h时,求内接圆柱上方的圆锥的体积V;
h时,求内接圆柱上方的圆锥的体积V;