题目内容
已知一个圆锥的底面半径为R,高为h,在圆锥内部有一个高为x的内接圆柱.
(1)画出圆锥及其内接圆柱的轴截面;
(2)求圆柱的侧面积;
(3)x为何值时,圆柱的侧面积最大?最大侧面积为多少?
(1)画出圆锥及其内接圆柱的轴截面;
(2)求圆柱的侧面积;
(3)x为何值时,圆柱的侧面积最大?最大侧面积为多少?
分析:(1)利用圆锥画出圆锥及其内接圆柱的轴截面;
(2)利用条件结合圆柱的侧面积公式求圆柱的侧面积;
(3)利用二次函数的图象和性质求圆柱的侧面积的最大值.
(2)利用条件结合圆柱的侧面积公式求圆柱的侧面积;
(3)利用二次函数的图象和性质求圆柱的侧面积的最大值.
解答:解:(1)如下图:
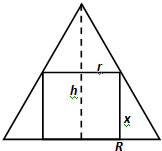
(2)设圆柱的底面半径为r,
则
=
,
∴r=
•R=R-
•R.
∴圆柱侧面积S=2πr•x=2π(R-
•R)x=-
x2+2πRx(0<x<h).
(3)由(2)知:圆柱侧面积S=-
x2+2πRx=-
(x-
)2+
(0<x<h)
∴当x=
时,圆柱侧面积最大,最大侧面积为
.

(2)设圆柱的底面半径为r,
则
| r |
| R |
| h-x |
| h |
∴r=
| h-x |
| h |
| x |
| h |
∴圆柱侧面积S=2πr•x=2π(R-
| x |
| h |
| 2πR |
| h |
(3)由(2)知:圆柱侧面积S=-
| 2πR |
| h |
| 2πR |
| h |
| h |
| 2 |
| πRh |
| 2 |
∴当x=
| h |
| 2 |
| πRh |
| 2 |
点评:本题主要考查圆锥和圆柱的侧面积的计算,利用一元二次函数的单调性求侧面积的最值是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 已知一个圆锥的底面半径为R,高为H,在其中有一个高为x的内接圆柱. 如图所示.
已知一个圆锥的底面半径为R,高为H,在其中有一个高为x的内接圆柱. 如图所示. 如图,已知一个圆锥的底面半径为R,高为h,在其中有一个高为x的内接圆柱(其中R,h均为常数).
如图,已知一个圆锥的底面半径为R,高为h,在其中有一个高为x的内接圆柱(其中R,h均为常数). 如图,已知一个圆锥的底面半径为R=1,高为h=2.,一个圆柱的下底面在圆锥的底面上,且圆柱的上底面为圆锥的截面,设圆柱的高为x.
如图,已知一个圆锥的底面半径为R=1,高为h=2.,一个圆柱的下底面在圆锥的底面上,且圆柱的上底面为圆锥的截面,设圆柱的高为x.