题目内容
【题目】已知椭圆
的离心率为
，且过点
．
（1）求椭圆
的标准方程；
（2） 设直线
与
轴交于点
，点
关于直线的对称点
在椭圆上，求
的取值范围.
【答案】（1）
；（2）
.
【解析】
（1）a=
解得c=2,即可得到椭圆方程；（2）设点
，线段
的中点
的坐标为
，直线的斜率
，直线
，直线
的斜率为
，且过点，设直线的方程为：
， 得
，
由
，得
，化简，得
,
进而得
,运用基本不等式求最值即可.
（1）由椭圆过点
可知
由离心率可知
，解得
所以
所以椭圆
的方程为.
（2）由题意，直线的斜率存在，设点
，
则线段的中点的坐标为，且直线的斜率
，
由点
关于直线的对称点为
，得直线，
故直线的斜率为，且过点，
所以直线的方程为：，
令
，得
，则 ，
由，得，化简，得
所以
.
当且仅当
，即
时等号成立.
所以
的取值范围是.
精英口算卡系列答案
应用题点拨系列答案【题目】近来国内一些互联网公司为了赢得更大的利润、提升员工的奋斗姿态，要求员工实行
工作制，即工作日早
点上班，晚上
点下班，中午和傍晚最多休息
小时，总计工作
小时以上，并且一周工作
天的工作制度，工作期间还不能请假，也没有任何补贴和加班费．消息一出，社交媒体一片哗然，有的人认为这是违反《劳动法》的一种对员工的压榨行为，有的人认为只有付出超越别人的努力和时间，才能够实现想要的成功，这是提升员工价值的一种有效方式．对此，国内某大型企业集团管理者认为应当在公司内部实行工作制，但应该给予一定的加班补贴（单位：百元），对于每月的补贴数额集团人力资源管理部门随机抽取了集团内部的
名员工进行了补贴数额（单位：百元）期望值的网上问卷调查，并把所得数据列成如下所示的频数分布表：
组别（单位：百元） |
|
|
|
|
|
频数（人数） |
|
|
|
|
|
（Ⅰ）求所得样本的中位数（精确到百元）；
（Ⅱ）根据样本数据，可近似地认为员工的加班补贴X服从正态分布
，若该集团共有员工
，试估计有多少员工期待加班补贴在
元以上；
（Ⅲ）已知样本数据中期望补贴数额在
范围内的
名员工中有
名男性，
名女性，现选其中名员工进行消费调查，记选出的女职员人数为
，求的分布列和数学期望．
附：若
，则
，
，
．
【题目】黄冈市有很多名优土特产，黄冈市的蕲春县就有闻名于世的“蕲春四宝”
蕲竹、蕲艾、蕲蛇、蕲龟
，很多人慕名而来旅游，通过随机询问60名不同性别的游客在购买“蕲春四宝”时是否在来蕲春县之前就知道“蕲春四宝”，得到如下列联表：
男 | 女 | 总计 | |
事先知道“蕲春四宝” | 8 |
|
|
事先不知道“蕲春四宝” |
| 4 | 36 |
总计 | 40 |
|
|
|
|
|
|
|
|
|
|
附：
写出列联表中各字母代表的数字；
由以上列联表判断，能否在犯错误的概率不超过
的前提下认为购买“蕲春四宝”和是否“事先知道
蕲春四宝
有关系”？
从被询问的
名事先知道“蕲春四宝”的顾客中随机选取2名顾客，求抽到的女顾客人数的分布列及其数学期望．
【题目】电视传媒公司为了了解某地区电视观众对某类体育节目的收视情况，随机抽取了100名观众进行调查．下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图：
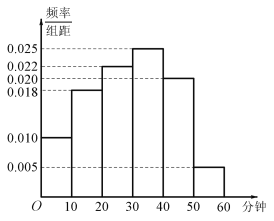
将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”．
（1）根据已知条件完成下面的2×2列联表；
（2）根据此资料，判断是否有
的把握认为“体育迷”与性别有关？
非体育迷 | 体育迷 | 合计 | |
男 | |||
女 | 10 | 55 | |
合计 |
附：
，其中
.
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
【题目】现有某高新技术企业年研发费用投入
(百万元)与企业年利润
(百万元)之间具有线性相关关系,近5年的年研发费用和年利润的具体数据如表:
年研发费用 |
|
|
|
|
|
年利润 |
|
|
|
|
|
数据表明与之间有较强的线性关系．
(1)求对的回归直线方程；
(2)如果该企业某年研发费用投入8百万元,预测该企业获得年利润为多少?
参考数据:回归直线的系数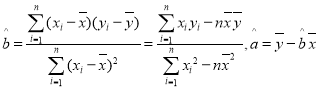
．